I began my work on this problem by using C2A to generate plots of the sky for the early evening of each day from 19th to 23rd December inclusive. In order to be able to easily compare each view, I set the time interval to one sidereal day rather than one solar day, thus ensuring that the background stars would remain unmoved from one image to the next. I also set the viewing mode to "Field" (which is the term C2A uses for what would normally be called "equatorial", in other words the view one would get through a telescope using an equatorial mount) rather than "Horizon" (the view one would get with the naked eye) so the true motion of the planets would not be affected by that produced by the rotation of the Earth: this also meant I could use the planets' positions as given by their astronomical Right Ascension and Declination coordinates in my calculations.
Having generated the plots I then experimented with various ways of combining them, working towards an application of the geometric method of finding the time of closest approach. Combining plots made without centring on any planet showed that the sky-paths of the two were very close to parallel, knowledge which would come in useful later. However, because the composite consisted of just the five positions of each planet there was no obvious way of determining when they would be closest together when traversing these sky-paths in a continuous manner. I thus moved on to combining views centred on Jupiter (as per the description of the geometric method, above) as it seemed all I needed to do then was to draw a line through each successive position of Saturn and then a further line beginning at the stationary Jupiter and meeting the first one at right-angles: this line would be the minimum distance between Jupiter and the track of Saturn and so where it cut Saturn's track would indicate the time of closest approach. Not so easy though, as drawing a line from exactly the centre of Jupiter at exactly right angles to the track of Saturn was difficult to achieve with precision. I thus felt I was not really making progress. However, an (email) conversation with Roger, my erstwhile school chum and current astronomical collaborator, indicated that he had had the same idea as me but had been more lucky with the weather and so had been able to capture more photographic observations than I had. He was hoping to use these to carry out a geometric method analysis, and so it seemed sensible for me to leave him to it and move on to considering the Zeno method.
The Zeno method is conceptually much easier to apply than the geometric method, as it basically relies on mathematics rather than "drawing". The only measurements that need to be taken from the generated plots are the positions of the planets as defined by their x- and y‑coordinates on the grid of pixels making up each image, and these can be read off directly using the cursor or a "rectangular selection marquee" in an image processing program. In fact, it is only strictly necessary to make two such measurements from each of just two plots: one giving the position of each planet on a date prior to the conjunction and one at a date after the conjunction. The distance each planet moves between these positions divided by the time interval used gives their speed along their sky-tracks and the difference in position between the two planets at the first date gives the head start that the slower has over the faster. The coordinates taken from each plot can be directly compared because using a time-step of one sidereal day ensures that the stellar background remains stationary. There is thus no need to construct a composite plot before taking the measurements.
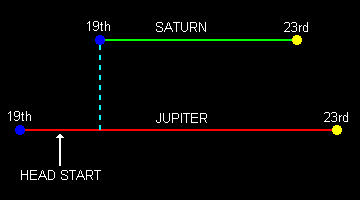
Complications arose immediately of course! Because the sky-tracks are inclined to the horizon the differences in position would apparently need to be calculated by applying Pythagoras' Theorem using both the x- and y‑coordinates. Also, the same problem as existed with the geometric method would exist here - measurement of the head start would involve constructing a line from Saturn down at 90deg to the track of Jupiter. Fortunately, I suddenly realised that the problem can be made much easier by simply rotating the plots so that the sky-tracks run purely horizontally. As the tracks of the two planets are very close to parallel (as mentioned above), a single amount of rotation will suffice to align the tracks of both. Rotation does not affect the overall geometry of the situation but makes the distances merely the difference in the x‑coordinate values. This can be seen by reference to the diagram below, where each planet starts off at the blue mark on 19th December and moves right each day (at different speeds) to arrive at the yellow mark on the 23rd. Whatever the actual "in the sky" slope of the sky-tracks, once the plot is rotated so the tracks are horizontal it is easy to calculate the distances required. Obvious in retrospect of course, but even the most obvious things do need to be thought of!

I wasn't quite there yet though, as when I tried to determine the exact pixel coordinates required it became obvious that the shapes representing the planets on the C2A plots were not sitting with their centres precisely over a single pixel position, mainly because they were composed of just a limited number of pixels. Add to this the fact that the shapes were irregular and it's not even easy to say where the centre actually is in the first place. Some estimation would therefore be necessary. Both these problems could be lessened if more pixels were present and so before reading the coordinates I resampled the plots to four times their original size. This gave me a much better estimate of which pixel was at the exact centre.
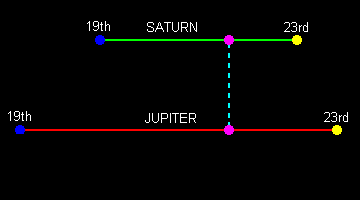
Once the distances are known, one can proceed either by arithmetic or by algebra. The arithmetical method works in a similar way to the actual Paradox, shifting each planet leftwards from its starting position by the amount each would move in a given short time interval until Jupiter has just caught up with Saturn, as in the diagram below. Adding the start time to the cumulative time Jupiter has taken to move from the start to this position gives the time of closest approach. The algebraic method starts with equations defining how far each planet has moved since the start and then restructures them to give an expression for the time it takes for Jupiter to catch Saturn. The final answer is that (perhaps surprisingly) this time is equal to the head start divided by the difference in their speeds, and does not depend on the total distance travelled.
And so it was time to roll out the spreadsheet - and after the various manipulations of the C2A plots this was the easy bit! Once I had entered the pixel values for the various measurements I had taken, I used these to calculate the head start and the total distances travelled, and from the latter the speeds. I then built a series of cells to use these values to implement the "incremental movement" algorithm as in Zeno's Paradox. I obviously didn't start this right back at 19th December, but rather at a time much nearer to when the closest conjunction would occur in order to cut down on the number of cells. Each row of the spreadsheet in this section gave the total distance travelled so far by each planet, with the final cell in the row showing the difference between them. When this reached zero I had my answer! I also calculated the algebraic answer, just as a cross-check.
So, after all this work, what did I find? Well, the Zeno method came out with the result 18:23:56 on the evening of 21st December. I felt this was definitely in the right ball-park but due to the variability in the times given online I could not be sure. I thus needed some sort of cross-check. As mentioned in the introduction, I couldn't use C2A for this so turned to Solex. I set the program to show the Right Ascension and Declination celestial coordinates for both Jupiter and Saturn at around the time of the conjunction, and from them (using Pythagoras' Theorem) calculated the separation between the planets. I then altered the time until I homed in on the instant where the separation was least. This time (to the nearest 15sec) was 17:53:45, at 367.853192 arc-seconds separation (I told you Solex was high precision!). Hmm. Half an hour different from my answer. I was thus reasonably close, but not particularly so. Given the care I had taken to get my base data correct, this was something of a disappointment. No obvious reason for this discrepancy occured to me, so I began to wonder whether my basic theory was correct.
While I pondered this issue, I re-visited the geometric method as of course I could apply the rotation idea to this method also. I thus rotated the composite image by the same amount I had used previously, drew a line through all the Saturn positions and drew a second line straight up from Jupiter to meet the first one. I measured Saturn's x-coordinate at the extreme positions of its sky-track (i.e. on the 19th & 23rd) and also the x-coordinate where the line from Jupiter crossed it. Together with the (known) time interval between the positions on 19th and 23rd I then had all the data I needed to calculate the time of closest approach. Putting in the numbers, the answer I got was 18:09:54. Again not far off the Solex value and actually closer than the Zeno method, something I found rather surprising, but still not particularly accurate.
I thus felt I had to move on to method 2B, where all calculations are done using Right Ascension (RA) and Declination (Dec) coordinates - for which I again used values generated by Solex. These will be inherently more accurate than pixel values, as no estimation of centres etc. is required, and of course the values provided by Solex are the most accurate one can get anyway, so in principle the answer should also be more accurate. However! The huge downside to doing it this way is that the rotation trick cannot be used, meaning that all distances would have to be calculated using Pythagoras' Theorem on the RA and Dec values. Also, and much more importantly, the "how to draw a line down from Saturn at right angles to the track of Jupiter" problem has to be faced head on.
Drawing on my somewhat limited knowledge of geometry (plus a bit of sneaky online research!) I was able to generate an equation which defined a line intersecting another line at 90 degrees and also passing through a specified point. I won't bore you with the details as the derivation is a bit lengthy, but suffice it to say that this equation allowed me to calculate the coordinates of the crossing point of the infamous line down from Saturn meeting the track of Jupiter at 90deg. This enabled a calculation of the head start which, together with the other distances calculated via Pythagoras, got me to essentially the same situation as for the 2A version of the Zeno method. I thus set up another worksheet and plugged in the values. The answer this time was 17:38:27 - slightly closer than any previous value, but still not accurate. This was getting frustrating.
The final throw of the dice was to use the 2B method but with everything put into spherical coordinates, in the hope that the problem lay in the way I was effectively flattening out what I have previously called the "sky dome" - that is, although the star field above us is best represented by a hemispherical surface I have been calculating as if the sections of sky under consideration are flat. They are nearly flat, to be sure - being just very small areas of a very large hemisphere - but they are not exactly so. Maybe this slight curvature was upsetting the geometry.
This transformation really confused the issue though! No longer could I use Pythagoras' Theorem as the triangles I was using now have curved sides - I would have to use the Napier Rule instead (lots of sines involved!). Neither could I simply subtract two values to get a distance - I would have to use a version of the spherical cosine rule because in spherical geometry distances are specified in angular measure. And of course I couldn't use a simple "y/x" formula to calculate the slope of a line either! Lots of typing later I hoped I had changed everything correctly, so I plugged in my measurements with great hopes of an improvement. Which were immediately dashed! However, I then realised I had made a logical error in one of the Pythagorean formulae which I hadn't noticed before as it didn't affect the final answer. It was clear it would seriously affect the spherical geometry calculation though, and indeed when I corrected it the time given was much closer to that given by Solex but it still wasn't all that close.
The only element of the calculation which was not now in spherical form was the equation I used to find the intersection of the line down from Saturn to the path of Jupiter, which was clearly going to need an entirely new approach. I thus broke out my secret weapon - pencil & paper! By drawing diagrams I was able to derive a several-step method to determine the head start from angles and distances already known - I hoped! This was quite a complicated process so I won't explain it here but it did enable me to determine, as part of the process, the "spherical" distance between Jupiter and Saturn on the 19th, which agreed exactly with the value given by C2A. This gave me added confidence that my method was sound. And it certainly helped the calculation, which now gave a time of 18:13:55 as compared to the Solex time of 18:27:38 when using spherical geometry - much closer.
Unfortunately, at this point I had run out of ideas as to how the situation might be further improved, so again I even began to question whether the basic theory behind what I was trying to do was sound. I also tried a bit of "working backwards from the answer", comparing the actual distances travelled by the two planets from 19th December to the Solex-generated time of closest approach, calculated from their known RA & Dec coordinates at these times, with the same distances as calculated by my spreadsheet. I also looked at the head start distance, using a similar approach. I found that these distances were nearly, but not quite, the same and the error was different for each planet. This was rather strange as my calculations were based on the same starting RA & Dec coordinates together with speeds derived from other clearly correct coordinates and a known time interval, so how could there be a discrepancy?
It was when I was washing up that I had my "Eureka!" moment, which was that the motion of any planet across the sky is not uniform! However, the Zeno method assumes that each "contestant" moves at the same speed throughout the "race". I had calculated the speeds using the full span of the C2A plots, from 19th to 23rd December, but if each planet moved faster between 21st & 23rd than between 19th & 21st the average speed from 19th to 23rd would be greater than that during the interval of the "race", leading to an earlier calculated time of closest approach. Also, if the increase in speed for Jupiter was different from that for Saturn that would account for the different degrees of error for the two planets. I really felt this must be the answer, and when I re-did the calculations using the positions on 19th & 21st rather than 19th & 23rd the speeds reduced by around 0.5%, and the ratio of the speeds of the two planets changed by about 0.2%, confirming both my conjectures. The time of closest approach now came out as 18:20:39 - much better, and in fact the closest so far (‑7 mins different from the Solex value). Encouraged by this breakthrough, I applied the same "variable speed" principle to the 2A (flat geometry) version of the Zeno method which resulted in a time of 17:43:42 - a difference of ‑10 mins from the Solex value, which was again a considerable improvement. I also applied it to the geometric calculation using a rotated version of the composite image of the C2A plots centred on Jupiter, which also resulted in an improvement, giving a time of 18:04:03 - an error of +10.3 minutes as compared to +16.17 without the speed adjustment.
Close though these results were, they were still not as accurate as I had hoped but I had now entirely run out of ideas as to how they might be further improved. I thus decided to try a bit of "sensitivity analysis", to see how much variation in the base parameters would be needed to get a totally accurate result.
In the case of the flat geometry version of the Zeno method, given that the planetary positions were defined by (presumed accurate) RA & Dec values, the only parameter I could easily vary was the angle at which the line down from Saturn intercepted the track of Jupiter, initially assumed to be 90 deg. I found that by decreasing the slope of the line by just 0.46 of a degree (0.6%), which produced an increase in the head start of just 0.35%, the calculated time would be precisely that given by Solex. In the case of the spherical geometry version, because the line down from Saturn was defined by reference to other calculated values rather than by means of an equation, it was easier to change the head start directly. I found that increasing it by just 0.24% produced a time exactly equal to the Solex-calculated value. As in the flat geometry case, this increase in head start could only be achieved by changing the slope of the line down from Saturn, but due to the way the head start was calculated I didn't think I could easily determine this change.
These changes show how sensitive the final answer is to extremely small changes in the data, but given that this data was produced by the most accurate astronomical program in existence I must assume that it is correct. The only free parameter in my entire calculation (whether using method 2A or 2B) is the head start, defined by the line down from Saturn to the path of Jupiter. It is obvious that this line must intersect the path at 90 degrees in the simple Zeno Paradox scenario (as per the diagram I showed) and so I had assumed it must also be the case in the "real world" of the celestial dome. That this seemed not to be the case was very puzzling but, at this stage at least, I had no real idea where the problem lay.
Having got as far as I felt I could with "RA & Dec" methods, I checked to see what progress Roger had been making with the geometric method. Quite a lot, as it turned out, some of which would be directly applicable to the calculations I had been doing with pixel values.
Roger had been puzzled by the fact that he could not accurately align his photographic images with plots produced by his astronomical program of choice, Stellarium. He eventually deduced that this was because the scale factor of each of the Stellarium plots (in terms of their "arc-seconds per pixel" ratio) was not quite the same. This was not entirely unexpected, as some degree of rounding error is inevitable when positioning objects whose coordinates have a (theoretically) infinite number of significant figures onto a grid having only a relatively small number of pixels. The effect this rounding has on the plotted position will vary from plot to plot and object to object, resulting in the observed variation in scale factor. The consequence is that when plots are stacked together each object will acquire a very slightly different shift from its true position as compared to its neighbours, thus making accurate alignment to a stack of photographic images impossible.
The effect will also invalidate the comparison of measured (pixel) distances between individual plots of course which is, on the assumption that what Roger found with Stellarium is also true for C2A, of great relevance to my calculations based on this principle. For example, I said above that the pixel coordinates on the C2A plots for 19th & 23rd December would be directly comparable because the stellar background had been made static. However, if the scale factors for the two plots were not the same then this would not be true. Discrepancies in pixel coordinates produce discrepancies in distance, and these then knock on to discrepancies in speeds. No wonder my results were not particularly accurate!
Once I had been alerted to this issue I could take steps to allow for it. I quickly confirmed that the C2A plots did indeed exhibit the problem (by comparing distances derived from RA & Dec values to those derived from pixel coordinates) so I constructed a table giving, for each plot, its individual scale factor and the multiplier needed to convert that factor to one representing the average across all the plots (which I hoped would give a better measure of the "true" distances). As previously mentioned, the Zeno method only really used the plots for 19th & 23rd December, with the head start lying entirely on the plot for the 19th and the distances moved for each planet (and hence their speed) lying partly on each plot. I thus corrected the head start by reference to the multiplier for the 19th and the distances by a composite muliplier derived by using the multipliers for the two dates in the same proportion as the parts of the distances which lay within those plots (which of course is different for the two planets).
The effect that these corrections had on the final result was dramatic! The time of closest approach now came out at 17:47:08, just 6.6 mins different from the Solex value as compared to over 30 mins before. When I also added in the correction I had found earlier - that the planets' speed from 19th to 21st was less than their speed over the entire interval from 19th to 23rd - I was overjoyed by the result. A time of 17:52:57, a mere 48 seconds away from the Solex figure!! Maybe the pixel-based Zeno method could be used to give an accurate result after all. I thus returned to the issue with the "90 degree intercept" which I described earlier.
My further thoughts were triggered by an observation I had made while applying rotation to the images in the pixel-based Zeno method. Even at the optimum degree of rotation the line through the positions of the planets did not pass exactly through all their centres i.e. their sky-tracks were not exactly straight lines. Also, although the tracks were very close to parallel they were not exactly so. Unfortunately, these are two of the requirements for the Zeno Paradox method to work correctly. The other of course is the assumption of constant speed, which has already been shown not to be true in the current investigation!
To deal with the "not straight lines" issue I tried working with the individual day-to-day segments of the tracks, not the overall end-to-end values. I calculated the slopes of each of these segments using the RA & Dec values and found that these did indeed change: in fact they increased by a significant 2% from 19th to 23rd December. Maybe I had found a reason for the difficulty in calculating the head start: if the tracks are curved then the "equation" method I used in the Pythagorean case would not work, as it assumed straight lines, and in the spherical geometry case the formulae only work if lines are curved simply because they lie along the surface of the sphere rather than veering off to "north" or "south" along the way. Unfortunately, coming up with a possible reason for a problem does not imply that one can then use this insight to solve the problem! There was clearly no simple way to correct the Pythagorean method and my knowledge of spherical geometry is nowhere good enough for me to derive formulae which would work on this type of curved line. I thus concluded that I would have to cease my analysis of the effect that a curved path would have at this point.
While the tracks showed a noticeable degree of curvature, the extent to which they were non-parallel was much smaller - only about one-tenth of a degree in fact. However, even this tiny amount did have a considerable effect on the final result. To estimate this, I utilised the work on sensitivity analysis I had done previously - see below.
A halt to the theory, that is, but not quite a halt to the calculations. As mentioned above, I felt I had to use the slope from 19th to 20th December in my head start calculations rather than that over the whole period to the 23rd. Unfortunately, this made the final answers less accurate! Ah well, you can't win 'em all. The times were 17:42:53 for the Pythagorean version (‑10.86 mins) and 18:17:58 for the spherical version (‑9.66 mins). The percentage increase in head start value needed to get the Solex-approved answer was 0.380% and 0.334% respectively - still extremely small values, representing a change in slope of half a degree. It can be seen that, interestingly, the use of the slope for 19th->20th in both cases has resulted in very similar errors and necessary correction factors. I feel this is probably significant and does point to a similar underlying cause - almost certainly the "curved straight line" issue.
As mentioned at the end of the previous section, I "took the easy way out" when it came to estimating the difference non-parallel tracks would have. In this case, instead of the line joining the tracks needing to intercept them at 90 degrees, as would (in theory!) be required with parallel tracks, it would have to sit at right-angles to a line running along the mid-point of the (very slightly) converging tracks. This would result in it meeting the tracks at a fraction less than 90 degrees, thus increasing the head start value a little. I could thus use my analysis just above, but scaled to take account of the much smaller angle. Perhaps surprisingly, this showed that even a convergence of one-tenth of a degree would add a couple of minutes on to the calculated time, to give 17:45:03 for the Pythagorean analysis and 18:19:54 for the spherical version, a difference of ‑8.70 and ‑7.73 mins respectively from the Solex value.
Having optimised the "Zeno Paradox" methods as far as I felt I was able, I turned my attention back to the geometric methods. I firstly revisited the calculation using the rotated C2A plots. I had initially used a rotation of 12.20 degrees but, based on my calculation of the day-to-day slopes of the planets' sky tracks, it was clear that this value could not really be justified as it was greater than the calculated values. I thus re-did the geometric calculation after using a rotation of 12 degrees, which generated a time of 17:51:04 - again less accurate than before (‑2.67 mins rather than just ‑48 seconds) but still closer than the Zeno method calculations by some margin.
I then looked again at the use of the composite image of the C2A plots centred on Jupiter, as I had realised that instead of trying to draw a line up from Jupiter which cuts Saturn's sky-track at exactly 90 degrees (difficult) all I needed to do was extend out a circle centred on Jupiter until it just touches Saturn's track (easy). The general idea is illustrated by the diagram below.
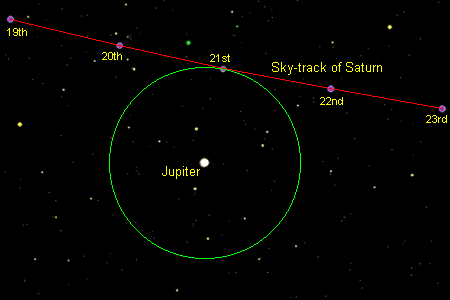
As with other plots, it was necessary to allow for the variation in the arc-sec/pixel scale before combining them. It was also again necessary to re-sample to 400% before taking measurements in order to get sufficient resolution, but even then determining exactly where two rather jagged single-pixel lines just meet was a matter of conjecture. So not quite so easy then! I finally decided on a "best guess" though, and was very pleased to find that when I calculated the time to which the intercept point corresponded I got 17:57:33 (+3.79mins). This time was, as usual, very sensitive to small changes in the measured pixel coordinates, a change of just 0.5px in either the measured position of Saturn on the 21st or the intercept point producing a change of 1.27mins in the final time - and that is 0.5px in the 4-times expanded version of course.
By this time my collaborator Roger had also come up with his version of this method but based on photographic captures rather than C2A plots. He had encountered further difficulties in that having discovered the variation in arc-sec/pixel scale in the plots from Stellarium which he was using to align his photographic images, he then found that these too were not quite consistent! A double correction was thus required. And if that wasn't enough, he also had to allow for the effect of atmospheric refraction on the position of the planets on his captures as the conjunction was quite low in the sky. It was therefore something of a triumph when he used the "expanding circle" method to generate a time of 17:57 - very similar to my estimate.
At this point I felt that enough was enough! Each method of determining the time of closest approach had proved to be full of numerous and unexpected problems which ultimately limited the accuracy of the calculations, with further practical difficulties constraining their precision. It had been a very useful learning exercise though, even if the original aim was not quite achieved.
| METHOD | RESULT | OFFSET |
|---|---|---|
| GEOMETRIC | ||
| Using a rotated composite of C2A plots centred on Jupiter, no corrections, "straight line" method | 18:09:54 | +16.15mins |
| Using a rotated composite of scale-corrected C2A plots centred on Jupiter, "expanding circle" method | 17:57:33 | +3.79mins |
| Using a rotated composite of scale-corrected actual observation images centred on Jupiter, "expanding circle" method (Roger's result) | 17:57 | |
| ZENO | ||
| Using individual rotated C2A plots for 19th & 23rd December, with the measurements corrected for scale errors and the result corrected for variation in speed | 17:51:04 | ‑2.67mins |
| Using Right Ascension & Declination coordinates, corrected for speed variation, in linear geometry | 17:52:57 | ‑0.80mins |
| Using Right Ascension & Declination coordinates, corrected for speed and sky-track slope variation & non-parallellism, in linear geometry | 17:45:03 | ‑8.70mins |
| As above but in spherical geometry | 18:19:54 | ‑7.73mins |
| ASTRONOMY PROGRAMS | ||
| Solex, linear geometry | 17:53:45 | |
| Solex, spherical geometry | 18:27:38 | |
| Estimate from C2A, spherical geometry | 18:26:30 | |
So, what can we learn from the above rather disparate results? Firstly, that applying the Zeno method has so many practical problems, with a whole range of corrections one might consider taking into account (some of which improve the result while others do not) that it's not really worth using when there is a very straightforward alternative available - the Expanding Circle Geometric method. This gives good results with almost no need for corrections other than just ensuring that the images used to generate the final composite from which to work are consistently produced. Also, it is capable of giving improved results the greater the pixel resolution of the images used, as the accuracy depends solely on an estimate of when one drawn line meets another rather than the complex calculations needed by the Zeno method. The fact that Roger & I came up with essentially the same result using totally different base images and working independently tends to support the view that the "ECG"method is accurate, repeatable and easy to use.
However, as there are results from the Zeno and Geometric methods which both used the same base data (the plots produced by C2A), it's perhaps not unreasonable to suggest that a final answer might be found by taking an average between them, which comes out to 17:54:19, just 1.12 minutes later than the Solex answer. This compares very well to the spherical geometry estimate derived from C2A which was 1.13 minutes early. Probably just a happy coincidence, but I'll take that!
But what, I hear you say, is the correct answer? At what time was the conjunction actually at its closest? In a numerical sense this has to be given by the times produced by Solex, as it gets its results by numerical integration rather than from observations and thus avoids the myriad problems inherent in the latter. But which of its answers? Well, that all depends on your viewpoint (in both a literal and a metaphorical sense). As previously mentioned, for an observer on the Earth all the celestial bodies seem to be moving across the surface of a hemispherical dome above our heads, with us at its centre. When viewing a small section of this dome one's impression is that everything is on a flat sheet rather than a curved surface, and of course for photographs of the night sky or plots produced by planetarium programs this is literally true. In this situation it is only the planets' motion across the plane which is noticeable and so the conjunction would appear to be at its closest at the time given by the linear geometry ("Pythagorean") version of the Solex calculation. In truth though, the surface upon which the celestial bodies appear to move is actually part of a very much larger sphere with the Earth at its centre - rather like the "crystal spheres" model put forward by early astronomers as part of the geocentric theory of the solar system. It should be clear that although the planets would move across the observer's dome and the "crystal sphere" in a rather similar manner, because the centres of these imaginary items are not at the same point in space the planets' tracks across them would not be quite the same. Crucially for my calculations, the Right Ascension / Declination coordinate system is based on the "crystal sphere" and not the observer's dome and so any calculation fully based on these coordinates (i.e. those using a geocentric spherical geometry model) will be slightly different from that using the observer-centric "flat sheet" model. So, if we are talking about the practical case of someone on the Earth's surface looking up at the skies the closest approach would have been at 17:53:45. If on the other hand we are considering the rather hypothetical case of "the Earth goddess" observing the conjunction in outer space then the time would have been 18:27:38.