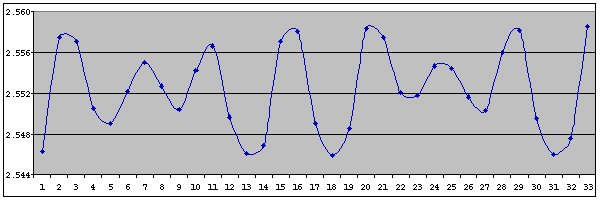
Figure 1. The perihelion distance of successive orbits of Ceres
| Variations in the perihelion distance of dwarf planet Ceres, caused by perturbations by Jupiter, were analysed using geometric and mathematical models to give a theory describing their periodicities. The conclusions reached were verified by comparison with a large dataset of calculated values. The methodology was then applied to the orbits of other asteroids, giving very good agreement with actual data. |
The opposition of the asteroid and dwarf planet Ceres in early 2009 was widely reported as being the nearest since 1857. While investigating this statement (and finding it to be true!) I became aware of the significantly large variations in the distance of Ceres from the Sun, and indeed in all other parameters of its orbit. These variations clearly had a periodic component, but one whose precise origin was not obvious. I thus undertook a numerical analysis in order to determine the reason for the particular form of these variations. Having developed a comprehensive theory, I was then able to apply it to the similar variations in the orbits of other major asteroids.
The asteroid belt is in a rather delicate position in the solar system - small bits of rock orbiting close to the largest planet, Jupiter. Indeed, it is thought to be the influence of Jupiter that stopped the asteroids coalescing into a planet when the rest of the solar system was formed. Its strong gravitational attraction disturbs their orbits very substantially, meaning that every parameter (distance to the Sun, inclination, orbital period, orientation of the orbit etc.) is subject to periodic variations of significant proportions. If these perturbations build up from orbit to orbit they can even become large enough to eventually throw an asteroid completely out of position, resulting in it leaving the main belt. Build-up will happen if there is a simple relationship between the orbital period of Jupiter and that of the asteroid, so that Jupiter "tugs" on the asteroid at the same places in its orbit each time. For example, in a 3:1 resonance (as these relationships are called), the perturbations will always be exactly 180 degrees apart each time, leading to a rapid shift in orbital parameters.
A body's orbital period is determined by its mean distance from the Sun, so the end result of such resonances is to clear out asteroids whose orbital distance corresponds to a resonant period, thus leaving "gaps" in the asteroid belt. For example, the 3:1 resonance happens at a distance of 2.50 astronomical units (AU). The next two most significant resonances are 5:2 and 7:3, corresponding to 2.82 AU and 2.95 AU respectively. The gaps at these "forbidden" distances are called Kirkwood gaps, after the astronomer Daniel Kirkwood who discovered them (by coincidence, in 1857!). At 2.767 AU, Ceres is too far from the 5:2 resonance distance to be ejected but it will still experience significant disturbances. Figure 1 shows a typical example - the perihelion distance of successive orbits.

The periodicity of the fluctuations is somewhat irregular but averages out at about 41/2 orbits. We also see that the magnitude of the fluctuations is variable and probably periodic, though the periodicity is not clear. I felt it was reasonable to assume that the perturbations will be at their strongest when Ceres and Jupiter are closest together i.e. when they are in heliocentric conjunction. The average interval between such conjunctions is 1.634 orbits (of Ceres) and so the best match to the periodicity of 41/2 orbits shown by Figure 1 would be 3 conjunctions - this is 4.90 orbits however. So what's going on?
The answer to the above question lies in the fact that to affect the orbital parameters the perturbations need to be not only strong but also at the correct place in the orbit. Orbital mechanics tells us that a body's perihelion distance can most easily be changed by affecting its orbital speed at aphelion. To properly investigate the periodic variations we thus need to consider how far a given Ceres-Jupiter conjunction is from the point at which Ceres is at aphelion. A perturbation occurring during a conjunction exactly at aphelion will have the maximum effect on the perihelion distance but, because conjunctions do not happen at intervals of an exact number of orbits of Ceres, they will steadily fall out of alignment with aphelion: this will reduce the effect of the perturbations. For example, after a couple of 3-conjunction cycles (each cycle taking 4.90 orbits) the point of conjunction will have slipped out of alignment with aphelion by 0.2 of an orbit - enough that the alignment after just 5 conjunctions is actually better, leading to a greater perturbational effect after 5 conjunctions than after 6. To see this, observe that 2 conjunctions take 3.27 orbits. A sequence of 3+2 conjunctions will thus take 8.17 orbits - just closer to a whole number than the sequence 3+3 (9.81 orbits). Even if you want to call that one a draw, the situation after a further cycle of 3 is clear-cut: 3+2+3 is 13.07 orbits while 3+3+3 is 14.71 orbits [3+2+2 is just 11.44 orbits, so clearly does not come into consideration]. The conclusion is that although the greatest perturbational effects usually happen after an interval of 3 conjunctions, they sometimes do so after just 2. These "2's" make the periodicity of the fluctuations irregular (i.e. they are actually "quasi-periodic" rather than truly periodic) and decrease the average time between greatest effects. In fact, by extending the above analysis we find that the sum total closest to a whole number is given by eleven "3's" and four "2's" - 67.0075 orbits. The average "cycle time" for this sequence, 67 orbits divided by 15 conjunctions, equals 4.47 orbits (or 20.57yrs), which is the true value of the [average] periodicity shown by the perihelion distance graph.
While this result is pleasing, proving it conclusively took a little more work! However, the effort was worth it, as deeper analysis not only proved my assertion but also gave a reason for the fluctuations in the magnitude of the oscillations shown in Figure 1.
Hopefully a diagram, or indeed a series of diagrams, will start to make the process clearer. In Figure 2, Ceres is shown in blue with Jupiter in red. Both bodies are moving in an anti-clockwise direction, as shown by the arrows. Ceres' aphelion is presumed to be at exactly the "12 o'clock" point.
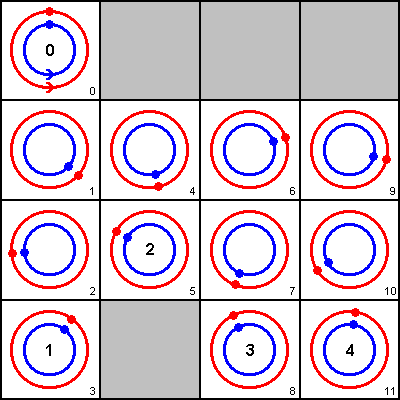 Figure 2. Diagrammatic illustration of a sequence of conjunctions | The sequence starts at top left, with the initial position - the first conjunction exactly at aphelion. Running down the first column are the positions after 1, 2 & 3 further conjunctions [it is to be understood that Ceres completes one full orbit plus almost two-thirds of a further orbit between conjunctions whereas Jupiter moves just the two-thirds]. It can be seen that both bodies are fairly close to the aphelion of Ceres again after the 3rd conjunction and so the effect on the perihelion distance will be quite large. The position after both 2 and 3 more conjunctions is quite similar (diagrams 5 and 6), but on opposite sides of the aphelion point. In fact, confirming the calculation given above, Ceres is slightly closer to aphelion after 2 conjunctions than after 3 (by just over 8 degrees) so the perturbation effect here will be just slightly greater. The next "close to aphelion" position arises 3 conjunctions after diagram 5, and the next is 3 conjunctions after that i.e. at diagrams 8 and 11 respectively. In these cases there is no question of the position after just 2 conjunctions being nearer than that after 3. The number of conjunctions between each "greatest perturbation effect" position is thus 3, 2, 3, 3. Note that if (as mentioned above) you deem diagrams 5 and 6 to be effectively the same and therefore want to count position 6 as being the best alignment after position 3, it is clearly the case that the position in diagram 8 is closer to aphelion than that given by diagram 9 and so the 2-conjunction interval still appears: it's just that the overall sequence is now 3, 3, 2, 3. |
This series of diagrams shows how the basic quasi-periodicity of the perihelion distance graph comes about. However, we saw above that, while the 4.47 orbit period is quite obvious, the variation in the height of the peaks also seems to have a long-period amplitude variation, with a period of 16 or 17 orbits (80yrs or so). To investigate this matter further I decided to construct a mathematical model, in order to eliminate any complications introduced by "the real world", to see if any longer-term patterns emerged. In a similar way to the method I used to produce the diagrams above, I calculated the angle between aphelion and conjunction for many successive conjunctions and plotted the results on a graph, shown as Figure 3.
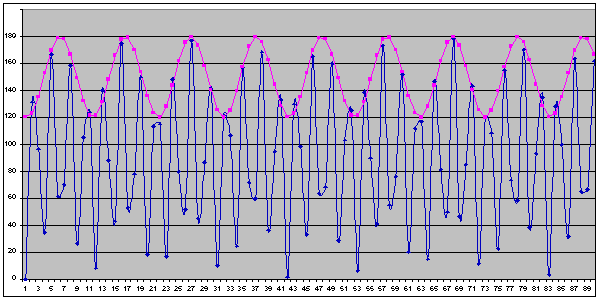
Looking closely at the graph [the blue curve] the first thing to note is that there are very low minima at points 1, 42 & 83. These are 41 conjunctions apart, and 41 conjunctions take 67 orbits i.e. the optimum alignment period described above is noticeable in the form of distinct minima at 41-conjunction intervals. These minima are particularly pronounced because of the almost exact alignment of aphelion and conjunction at those times. Secondly, note that successive minima are separated by either 3 or 2 conjunctions, also as found above. Taking the number of conjunctions between the "smallest minima" [i.e. points 1, 12, 23, 31, 42] the pattern is 3,2,3,3; 3,2,3,3; 3,2,3; 3,3,2,3. This is the total of 41 conjunctions already found, constituted from the basic patterns shown by the orbit diagrams above, with an overall large-scale structure of 11, 11, 8, 11. This pattern is also demonstrated by taking the next set of smallest minima [points 42, 53, 64, 72, 83]. In other words, the graph is quasi-periodic on a large scale, with periods of 11 and 8 conjunctions, as well as on a small scale with periods of 3 and 2 conjunctions, just as suggested by the perihelion-distance graph. The mean period of the sequence of 11, 11, 8 & 11 conjunctions, which I call the "super-period", is 10.25 conjunctions or 16.75 orbits which is 77.13yrs: this is the true periodicity of the long-term fluctuations. The pink curve superimposed on the top edge of the graph shows this: it has a period of 10.25 conjunctions and is an excellent fit to the large-scale oscillations in the data.
The emergence of the longer-term (quasi-)periodicity can also be seen by using orbit diagrams. I have combined all the smaller diagrams shown in Figure 2 into one - at top-left in Figure 4. The closest points to aphelion are marked 0, 1, 2, 3 & 4 and correspond to the same situations marked on the smaller diagrams. The green line indicates the position of Ceres' aphelion.
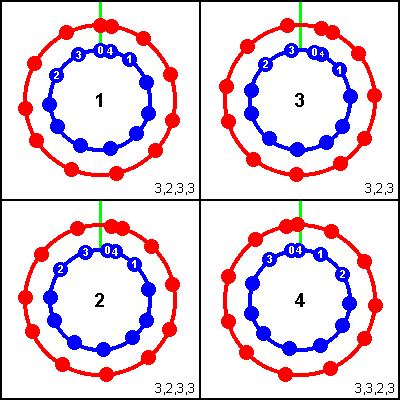 Figure 4. Orbit diagrams illustrating the "super-period" | It can be seen that, as demonstrated above, after 11 conjunctions the position is almost back to the start, but not quite - position 4 is 8.05 degrees before aphelion. Note that position 3 on diagram 1 is 26.87 degrees after aphelion. After a further cycle of 11 conjunctions [during which all the points will shift clockwise by 8.05 degrees] position 3 will only be 18.82 degrees after aphelion while the end position (position 4) will be 16.10 degrees before it - this is shown as diagram 2. The small difference means that when we arrive at position 3 after the first 8 conjunctions of the next cycle it will be closer to aphelion than position 4 would be if the cycle completed (shown by a small number). The cycle will therefore be truncated (as 3, 2, 3) after only these 8 conjunctions, giving diagram 3. The final position is still after aphelion, however (by 10.77 degrees in fact) and so after one more full 11 conjunction cycle it will be just 2.72 degrees after aphelion - this is diagram 4. This is "as good as it gets", as further final positions will clearly move further before aphelion, so the sequence ends here at 11, 11, 8, 11. Note, by the way, that because in the final cycle of 11 conjunctions the start position is just slightly after aphelion, the situation after 3 then 3 conjunctions is now closer to aphelion than the situation after 3 then 2 conjunctions. The sequence of conjunctions for the final cycle is thus 3, 3, 2, 3 i.e. it has both position 1 and position 2 before aphelion. This is the situation described at the end of the explanation for Figure 2, in the case where the alignment in diagram 6 is slightly better than that in diagram 5 due to the initial offset from aphelion. The same process can of course happen for diagrams 1 & 2 of Figure 4 as well as diagram 4, leading to them having the sequence 3,3,2,3. In this case, however, it turns out that diagram 4 will always have the sequence 3,2,3,3. The "super-sequence" can thus in fact be either 3233/3233/323/3323 or 3323/3323/323/3233 depending on the initial conditions. |
These composite diagrams clearly show how the 11, 11, 8, 11 cycle seen in the graph produced by the model comes about so, encouraged by the results given by the model, I used the Solex program of Prof. Aldo Vitagliano (University of Naples) to generate a whole new dataset giving the actual angle between the aphelion of Ceres and the point of conjunction for all the conjunctions between 1944 and 2696. And yes, I did need that many values! 41 conjunctions take over 300yrs and I felt I needed to plot more than one cycle to prove the point. Also, as it happened, the beginning of a clear cycle didn't happen for the first 90yrs. Plotting the results gave a graph that was so close to that generated theoretically (i.e. Figure 3) that it would be pointless me including it here. Not only were the most prominent minima in exactly the same places but the depths of the other minima were also the same. However, when calculating the actual angle I did have to allow for the fact that the longitude of the aphelion of Ceres will move noticeably over this extended timescale, due to perihelic precession: I shall return to this topic a little later. I was thus confident that my theoretical treatment was giving me a highly accurate representation of the actual situation, and so the results I had derived would also be accurate.
Having discovered the underlying mechanism of the two sorts of quasi-periodicity, in order to make further progress I moved on to consider the "osculating" values of orbital parameters. The osculating orbit is the orbit that would result if the motion of a body was to be undisturbed from this point forward i.e. it shows us what the perihelion distance (for example) would be if the body experienced no more perturbations until it got to the perihelion point. This is something of a mathematical abstraction of course but it should be remembered that the perturbations we are considering have their effect at the opposite side of the orbit from where they occur. The osculating value gives a better illustration of how the perturbations at aphelion are actually affecting the perihelion distance because it removes additional effects experienced on the way to perihelion from aphelion. These additional effects are the reason that the perihelion distance graph given as Figure 1 is rather irregular in form.
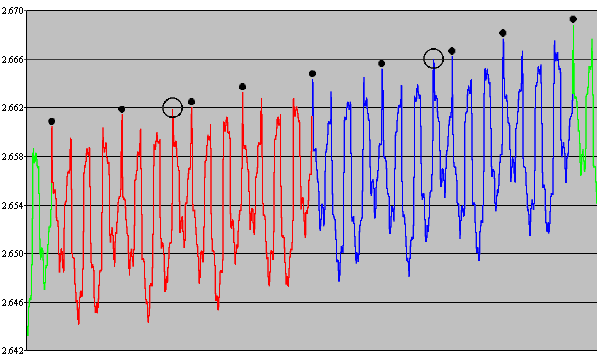
Figure 5 shows the osculating perihelion distance each 80 days from 1944 to 2621 - over 3000 data points! It is clearly far more regular than the original graph, permitting more detailed analysis. The steady increase in (mean) perihelion distance is due to a slow decrease in the mean eccentricity of the orbit of Ceres over this time-period as a result of the cumulative effect of perturbations on the other orbital parameters. It does not affect the conclusions reached so far as the analysis deals only with the relative magnitude of effects, not their absolute size.
The graph has been coloured and marked-up to highlight a number of important points:-
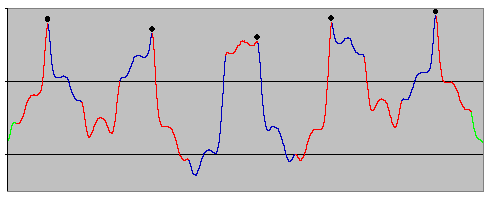 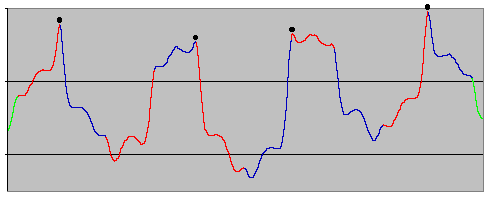 Figure 6. Expanded sections of Figure 5 | Figure 6 shows expanded versions of the first and third cycles of the blue section of Figure 5. The maxima are again shown by black dots but this time the red and blue sections mark the periods from one conjunction to the next. The first thing to note is that maxima do indeed occur at the time of conjunctions. It is clear that the pattern of number of conjunctions between the maxima is 3,3,2,3 in the upper diagram and 3,2,3 in the lower diagram, as calculated by me previously i.e. a total of 11 and 8 conjunctions respectively. Referring back to Figure 5, the second and fourth cycles of the blue section are clearly very similar to the first i.e. they contain 11 conjunctions. The overall pattern of each coloured section is thus seen to be 11,11,8,11, also as calculated previously. This pattern exactly accounts for the irregular spacing of the greatest maxima, the mix of 1 period of 8 conjunctions (60.20yrs) and 3 periods of 11 conjunctions (82.77yrs) leading to the 77.13yr additional (quasi-)periodicity stated. In addition, taken over the entire cycle of 3323/3323/323/3233, the mix of 4 periods of 2 conjunctions (15.05yrs) and 11 periods of 3 conjunctions (22.57yrs) again gives the 20.57yr basic (quasi-)periodicity. |
So, the "real-life" data confirms that the short-period and long-period variations are both due to the same cause - a consequence of the presence of alignment cycles of different periodicity. The 20.57yr (4.47 orbit) basic period is due to the need for cycles of both 3 and 2 conjunctions in order to synchronise conjunctions with aphelion, and the 77.13yr super-period is caused by there being cycles of 11 and 8 conjunctions in the angular distance between aphelion and conjunction (and thus in the effectiveness of the perturbing force) at such alignments.
When plotting Figure 5, I noticed that two maxima were anomalously high as compared to other similar maxima - these are marked with open circles. Suspecting this might have something to do with the orbit of Jupiter, I calculated the distance from Ceres to Jupiter at each graph point and found that at the anomalous maxima the conjunction distance was at a minimum even though Ceres was not close to aphelion. This is because of the varying distance of Jupiter from the Sun, due to the eccentricity of its orbit. These unusually small Ceres-to-Jupiter conjunction distances resulted in a larger perturbation than might otherwise have been predicted, causing the greater maxima. The anomalous maxima are separated by exactly the time interval equal to 41 conjunctions, as might be expected.
That this effect is caused by the varying distance of Jupiter can be seen by considering the celestial longitude of these conjunctions: 9.6 and 12.2 degrees respectively. The longitude of Jupiter's perihelion is around 15.6 degrees over the period of my study and there were only four conjunctions occurring near this point: two before it and two after it. Each pair was separated by the same 41-conjunction interval. The two before it were, on average, closer to the perihelion point of Jupiter than the two after (-5.9 & -3.5 degrees away compared to +5.2 & +7.1 degrees) and of course the two after were also further from the aphelion of Ceres (whose mean longitude was 338 degrees) so would have a slightly lesser perturbation effect anyway. It would thus seem likely that the two conjunctions happening just before Jupiter's perihelion would be the ones to be most affected by the nearer position of Jupiter, and indeed this is so - these were the conjunctions noted above. [All positions relative to equinox J2000]
I have already mentioned, when discussing the comparison of the theoretical analysis with the actual data for Ceres, that the motion of the point of aphelion due to precession does have a small but noticeable effect on the actual data. The extent of this shift is 54.07 arc-seconds per year or 1 degree every 66.58yrs. The shift in the 7.52yrs from one conjunction to the next is thus very small (just 0.113 degrees) and, because the angular difference between "good" and "bad" alignments of conjunction and aphelion is quite large, this amount of extra variation has no effect on the basic period sequence. However, in a 41-conjunction interval of 308.51yrs aphelion will have moved by 4.634 degrees. This is approaching twice the amount the final conjunction of the sequence of 41 is past the nominally-fixed aphelion (2.714 degrees) but, because the point of aphelion moves in the same direction as Ceres orbits, the two motions partially cancel out to give a final offset of 1.920 degrees before true aphelion rather than 2.714 degrees after it. Optimum alignment thus still occurs after 41 conjunctions (it's just that it happens after 66.99467 orbits rather than 67.00754) and so the super-period sequence is also unchanged.
This conclusion does not hold for other asteroids, however, as will be seen in the final section of this paper.
While it is true that the number of orbits in 41 conjunctions is indeed very close to a whole number, it is not exactly a whole number and so, as we have found, there will be an offset from perfect alignment of the final conjunction with aphelion of around 2 degrees (whether precession is taken into account or not). The question thus arises as to the effect this will have on the subsequent cycle of 41 conjunctions. We saw in Figure 4 that, in diagram 2, the angle of position 3 from aphelion differed only slightly from that of position 4. It would thus take only a small shift in the initial situation for position 3 to be closer to aphelion than position 4 and so cause diagram 2 to have the sequence 3,2,3. However, because the angular shift from one conjunction to the next is constant, an offset which moves a given conjunction nearer to aphelion will move the next one further away. This will cause diagram 3 to have the sequence 3,2,3,3 (or 3,3,2,3), changing the overall super-period sequence to 11,8,11,11. Any changes in the super-sequence caused by an imperfect starting point are thus largely "self-adjusting" because if an "11" changes into an "8", the subsequent "8" will always become an "11": there will therefore never be a sequence such as 11,8,8,11.
Eventually, however, the cumulative offset over a number of cycles will build up sufficiently to require a more drastic adjustment to the super-sequence, to get things fully back into synchronisation again. This is brought about by there being either one less or one more 11-conjunction element in one of the super-sequence cycles. Calculation shows that, taking precession into account, excellent long-term synchronisation can be achieved if one cycle in five drops an element and thus has only 30 conjunctions rather than 41 (in much the same way that the dropping of a 3-conjunction element produces the "8" in the super-sequence itself). Instead of successively repeating cycles of 41 conjunctions, the actual position is thus more like 41,41,41,41,30 / 41,41,41,41,30 etc. This mechanism reduces the cumulative error after each 194-conjunction cycle to just 0.302 degrees.
So is it reasonable to call the pattern 41,41,41,41,30 a "hyper-sequence"? My answer would be "no", simply for the pragmatic reason that it would be almost impossible to discern such a periodicity in the perihelion-distance graph. Firstly, its very long timescale (of almost 1500yrs) would require an enormous number of points to be plotted before anything might be seen. Secondly the pattern does not introduce a new and distinct modulation of the perihelion-distance graph in the same way that the basic sequence and super-sequence do. Any attempt to classify it in terms of a hyper-sequence is thus rather pointless. The best that can be said is perhaps that the hypothetical hyper-sequence should be used as a second-order correction to the long-term value of the super-sequence periodicity, so instead of 41/4 oppositions = 77.127yrs we should use 194/19 oppositions = 76.830yrs (a correction of about 0.4%).1
The above analysis concentrates on establishing the optimum condition for a maximum orbital variation to take place, without worrying about the details of the effect the perturbation has. For completeness, however, I think it's worth saying something about how a perturbation actually changes the orbital parameters.
One might naively think that a perturbation simply "stretches" the orbit as the smaller body is pulled slightly towards the larger. This cannot be true, however, as if it were how could the perihelion distance ever decrease? In fact, perturbations affect orbits by changing the speed of the orbiting body. Because the pull of Jupiter is at an angle to Ceres' orbit, the force can be resolved into two components: along the orbit and at right-angles to the orbit. While both components can change the orbital parameters, they affect different parameters and do so in different ways. For simplicity, I will only consider the "along the orbit" component: not only is this easier to analyse but also it is the component which has the greatest effect in changing the parameters we are interested in.
If Ceres is moving towards Jupiter (i.e. it is approaching conjunction) then the gravitational attraction exerted by Jupiter is in the same direction as Ceres' motion so it will speed up. Conversely, if Ceres is moving away from Jupiter (i.e. it is leaving conjunction) the force will be against its motion so it will slow down. Orbital mechanics tells us that an increase in orbit speed will lead to an increase in orbit distance of that part of the orbit diametrically opposite to where the speed increase occurred. In a similar way, a speed decrease will lead to a decrease in orbit distance. As conjunction is close to aphelion in the cases we are considering, theory says it is the osculating perihelion distance which will be affected, as we have found. I say "osculating perihelion distance" because of course Ceres hasn't got to perihelion yet so we can't speak about the actual distance. During a conjunction, the attraction (and thus the speed-up) will get greater as conjunction approaches and the distance between Ceres and Jupiter decreases, so the [osculating] perihelion distance will get steadily larger. As Ceres then moves away from conjunction it will be progressively slowed down again and so the reverse effect will happen - the [osculating] perihelion distance will steadily decrease.
The magnitude of the speed-up and slow-down (and hence the changes in osculating perihelion distance) will only be the same if conjunction is exactly at aphelion, however. The key point here is not so much the Ceres-Jupiter distance but the fact that, when it is at aphelion, Ceres will be moving more slowly than elsewhere. Thus if the conjunction is after aphelion, during the period before conjunction Ceres will be near to aphelion and therefore moving slowly, and so will be "under the influence" of Jupiter for a greater time than average. This will produce a greater speed-up before conjunction than slow-down after, when it will be well past aphelion and therefore moving faster and hence hurrying away from Jupiter. In this circumstance the perihelion distance will therefore increase more than it decreases. Conversely, if conjunction is before aphelion the situations will be reversed and so there will be a greater decrease than increase. While this difference would only be very small for a planet such as the Earth which has an almost circular orbit and thus little variation in its orbital speed, asteroids have much more eccentric orbits and so the effect is considerably larger.
All these cases are demonstrated in Figure 6 - particularly in the upper diagram. The shape of the first and last peaks is reasonably symmetrical, which should mean that these conjunctions are both very close to aphelion. The second peak has the shape for "conjunction before aphelion" - a greater decrease in perihelion distance after the conjunction than increase before it. The middle peak is fairly flat, which should indicate that neither of the nearby conjunctions is particularly close to aphelion. The fourth peak is clearly "conjunction after aphelion" - a greater increase in perihelion distance before the conjunction than decrease after it. Referring to the orbit diagrams (Figure 2) we see that these conclusions do indeed represent the actual situations. There is also evidence of the effect of the force at right-angles to the orbit I mentioned above, in the low part of the graph between the third and fourth peaks on the upper diagram and between the second and third peaks on the lower one. The conjunctions happening here are almost exactly at perihelion. As would be expected, this has almost no effect on the perihelion distance. There is a slight "bump", however, and this is caused by Jupiter directly pulling Ceres slightly towards it. The effect is only temporary though because orbital dynamics tell us that the ultimate effect of this pull is, rather strangely, to slightly reduce the perihelion distance.
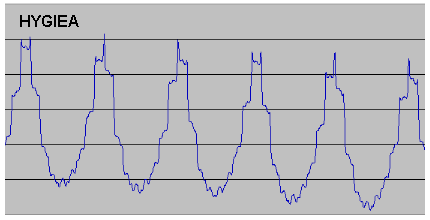
During my investigations of the above effects I discovered that the famous mathematical astronomer Jean Meeus was also working on problems connected with asteroid orbits for his book Mathematical Astronomy Morsels V. While discussing my findings with him he mentioned that other asteroids also exhibit periodicities in their perihelion distance, quoting 44yrs for Vesta and 91yrs for Hygiea. This intrigued me, as these values seemed rather large compared to their intervals between conjunctions with Jupiter (5.23yrs for Vesta and 10.50yrs for Hygiea). I thus decided to investigate!
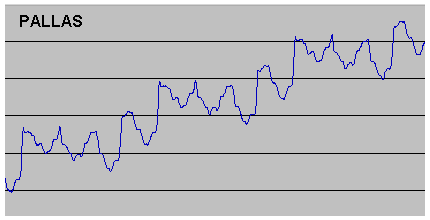
In the same way as I had done for Ceres, I used Solex to calculate osculating values and plotted them out. The results are given below, including data for asteroid Pallas as well, together with the plot for Ceres as a comparison. While there are great differences in the plots, the periodicities are very clear. [Note that the scales are different in each case, to enable the detail of the peaks to be clearly shown].
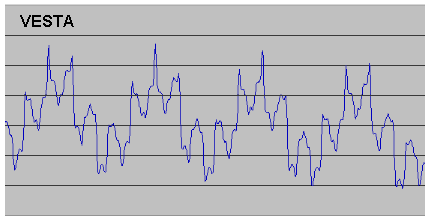
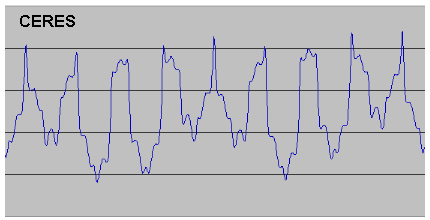
In the case of Vesta it was immediately apparent that the periodicity mentioned by Meeus was not what I have called the "basic periodicity" (20.57yrs for Ceres) but the "super-periodicity" (77.13yrs for Ceres). The super-periodicity is much more obvious for Vesta than for Ceres and so it could be taken for a basic periodicity, but the appearance of the smaller-scale fluctuations clearly shows this is not the case. Applying the same numerical analysis to Vesta as I had to Ceres resulted in the conclusion that for Vesta the super-period sequence should be 9,7,9,9,9,7,9,9,9,7,9 (93 conjunctions) made up of the basic period sequences 2,3,2,2 (=9) and 2,3,2 (=7). However, because of the large number of conjunctions in the super-period sequence, the shift of the point of aphelion due to precession has a much greater cumulative effect for Vesta than for Ceres. This results in the actual number of conjunctions between optimum alignments with aphelion being 59 rather than 93 and so the actual super-period sequence is truncated to 9,7,9,9,9,7,9.
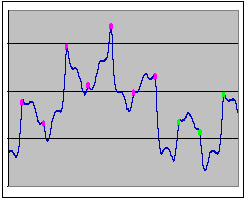 Figure 8. Perihelion distance graph marked up with points of conjunction | In addition, examination of the exact points on the osculating perihelion graph at which conjunctions occur (as was done in Figure 6 for Ceres) shows that the interval of 3 conjunctions in each basic period sequence is actually made up of three intervals of 1 conjunction each (see Figure 8 - the conjunctions in question are marked in green). This is a consequence of the fact that Vesta is close to the 3:1 resonance rather than the 5:2 resonance and so has a synodic period with Jupiter of almost 11/2 orbits rather than the very nearly 12/3 of Ceres. This means it is possible for there to be a conjunction not far before perihelion followed immediately by one not far after it.2 Recollect that, as explained in the section on the mechanism of orbit change (above), the shape of the perihelion distance graph around a given conjunction is strongly dependent on whether the conjunction is before or after aphelion. Remember also that perturbations near to perihelion itself do not affect the perihelion distance. While a precise analysis of the combination of these effects in the "before perihelion, then after" situation is complex, Figure 8 shows us that the overall result is to cause the graph to rise and then fall across these conjunctions, thus producing an unexpected peak between them (the one with the two green markers). |
The basic-cycle sequences for Vesta therefore have 5 peaks and 4 peaks respectively rather than the 4 and 3 predicted by numerical analysis: this is clearly seen in Figure 7. The basic periodicity is thus 9.35yrs and the super-periodicity is 44.08yrs (corresponding to the value given by Meeus). The offset after one cycle of the super-period is 0.82 degrees, meaning that the super-period sequence is substantially constant. None of the "9"s turn into "7"s (or vice-versa) after just a few cycles in the same way that some "11"s turn into "8"s in the case of Ceres, and none are skipped in the longer term. In fact the next "optimum alignment" period consists of no less than 447 conjunctions: no second-order correction to the super-period is therefore required.
The 1,1,1 sub-sequence doesn't just add an extra peak though. Because the conjunction before the pair spanning perihelion imparts a strong "conjunction before aphelion" shape (large fall, small rise) and one soon after a strong "conjunction after aphelion" shape (small fall, large rise), the mean level of the perihelion distance graph is lower during the 1,1,1 sub-sequence than during the 2,2,2 sub-sequence. This results in the graph having a more "up and down" appearance than that for Ceres, with its more equal rises and falls (very obvious in Figure 7), which is what makes the super-period for Vesta more apparent.
Hygiea is very interesting as there really does seem to be just one periodicity. However, again this is not the case - the basic periodicity is still there, but it is almost invisible! The reason for this is the fact that, because it is near the 2:1 resonance, the synodic period of Hygiea with Jupiter is close to a whole number of orbits of Hygiea (1.885, in fact). This means that it is not possible to apply the process whereby different multiples of the conjunction period can "compensate" for each other to give an overall result very close to a whole number of orbits and so keep the conjunctions in alignment with aphelion. Multiples of 1.885 simply get further and further away from a whole number, with the result that conjunction and aphelion drift apart very quickly. The osculating perihelion distance still changes of course (as the perturbations at each conjunction still have some effect) but as most of the perturbations will be far from aphelion there are few distinct short-period maxima in the curve and so we are left with only the super-period. This is still present because after 8 or 9 conjunctions the point of conjunction will have travelled right round the orbit and so will be near to aphelion again. There will then be 1 or 2 distinct maxima, visible as spikes in the graph, before alignment is again lost. The theoretical super-period sequence is 9,8,9,9 but because Hygiea has a more rapid perihelic precession rate than Ceres or Vesta (128.54 arc-seconds/yr) the point of aphelion moves considerably between conjunctions resulting in an actual sequence of just 9,8,9. This more rapid precession rate is in fact not a coincidence. There is a very strong effect associated with proximity to the 2:1 resonance, which can increase the rate by almost an order of magnitude: the analysis of this effect lies outside the scope of this paper, however. Calculation shows that the basic period is 10.50yrs (the period between conjunctions, as one would expect) and the super-period is 91.04yrs, again in agreement with the value quoted by Meeus.
Finally, I carried out the analysis for Pallas and once more there was some interest. Despite a steeply-rising baseline caused by a decrease in mean orbital eccentricity, the plot has the usual "greatest maxima" at intervals. This time, however, the repeating patterns of greatest maxima are identical, and they happen at perfectly regular intervals. These observations mean that the super-period is a true periodicity, not a quasi-periodicity made up of sequences of different lengths. This is because Pallas is slightly further from the Sun than Ceres, and so has a fractionally greater synodic period with Jupiter. A sequence of 3,2,1,2,3 conjunctions is now so very close to a whole number of orbits (17.99982, in fact) that no further "compensation" is necessary in the super-period. Perihelic precession has no part to play for Pallas because, very unusually, it is almost zero (probably because of the large inclination of its orbit: 33 degrees). Note that, because the "1" in the basic period sequence refers to the interval between two conjunctions spanning aphelion, rather than perihelion, it simply gives a flat top to one of the peaks, rather than producing a separate peak or trough as in the case of Vesta. Calculation shows that the basic periodicity for Pallas is 20.76yrs (very close to Ceres) and its super-period is 83.03yrs (greater than Ceres because its super-period is just 11 conjunctions rather than an average of the sequence 11,11,8,11 in the case of Ceres). The offset after one cycle of the super-period is a mere 0.064 degrees, confirming its stability.
I was pleased to find that the above results entirely support my explanation of the mechanisms behind both the basic period and super-period, and show that the theory can be used to describe very different behaviours of the osculating perihelion value. They also confirm that the values of the periodicities mentioned by Meeus for Vesta and Hygiea are in fact super-periods and not basic periodicities.
I would like to thank Jean Meeus for his many useful comments during the course of my investigations and also for his permission to paraphrase his analysis of the different shapes in the perihelion distance graphs3 for inclusion in this paper.
While the above results are all very neat and tidy, it is important to show that the theoretical analysis given is based on sound data and is robust to errors of reasonable magnitude and natural variations in this data.
The [sidereal] orbital period of Jupiter can be considered constant, though that does not mean it is well defined! I have taken the NASA value4 (4332.589 days), though slightly different values are quoted in other sources - many of these are actually the tropical period though. The most popular non-NASA value is 4332.71. The orbital period of Ceres is more of a problem however as, like all its orbital parameters, it varies considerably. The value I used (1681.601 days) was derived from the proper mean motion orbital parameter given on the Asteroids Dynamic Site (AstDyS)5: all other asteroid data in this paper came from the same source. This web-resource is maintained by the Space Mechanics group at the Dept. of Mathematics, University of Pisa, Italy and provides information and data on numbered asteroids including, importantly for my analysis, proper orbital elements (i.e. elements averaged over a very long timespan, free of periodic variations).
To determine the sensitivity of the analysis to the chosen values of the orbital periods I varied each of them until the 41-opposition interval did not give the optimum alignment i.e. until some other multiple of the synodic period was nearer to a whole number. I chose this criterion because it requires a very large change to the orbital period before the cycles of 3 and 2 oppositions making up the basic period will be disturbed: observe that although the orbital period of Pallas is well over 3 days longer than that of Ceres it has [fundamentally] the same basic-period sequence. Changes in the super-sequence are a much better indicator of sensitivity.
In the case of Jupiter, a value outside the range 4333.482 to 4330.950 was needed before the super-period was affected. This interval (2.532 days) is clearly much greater than the likely uncertainty in the orbital period and encompasses most of the other [believable] values given on the Internet. The conclusion, therefore, is that the results obtained by this analysis are robust to the effects of likely inaccuracies in the initial data for Jupiter.
For Ceres, the corresponding limits were 1682.238 and 1681.255 days. To assess the significance of these limits I derived values for the actual orbital period using Solex, to give me some idea of its natural variability (a variability caused, of course, by the effect on other orbital parameters of perturbations of the type I have been analysing). To do this, I determined the exact date (to 1 second) of instants of zero celestial longitude (relative to the fixed equinox of J2000) over the interval March 1961 to August 2269. While the particular start-date was chosen arbitrarily, the interval was selected to ensure that the results I got would not be skewed by the variability I was trying to estimate. The given interval, 308.47yrs, is in fact just 67 orbits of Ceres - the duration of the 41-conjunction repeat cycle quoted many times in this paper. Having calculated these instants, I then subtracted successive values to give a series of orbital periods: the individual values within the dataset ranged from 1682.701 to 1680.302 days. These were then averaged over a number of intervals chosen to demonstrate variability in the short, medium and longer term.
Grouping the values into appropriate sets of 5 and 3 orbits (corresponding to the sets of 3 and 2 conjunctions in the basic sequence) gave average orbital periods ranging from 1681.784 to 1681.396 days: these values are already within the limits given above. Averaging over each of the constituent sequences in the 67-orbit cycle (which divides up 18,18,13,18 in the same way as it divides up 11,11,8,11 when expressed in terms of conjunctions) gave results showing a very small variability: the averages were 1681.514, 1681.517, 1681.510 & 1681.502. The mean sidereal period generated by averaging over the entire dataset (1681.511 days) is close to that quoted by Meeus (1681.57)6, giving me confidence in the method used and also showing that the mean period does not vary greatly over the medium term. This is supported by a further statement by Meeus: in work on the orbital motion of Ceres from 1800 AD to 3000 AD7, he states that "The orbit's semi-major axis doesn't show any secular variation" [the orbital period is, of course, directly related to the size of the semi-major axis via Kepler's Third Law]. The value is also consistent with that given by AstDyS. Close agreement should not be expected due to the very different averaging periods, but this does show that the mean period is sensibly constant over a very large range of intervals of time. This conclusion holds for all the asteroids I have considered but the same is not true of, for example, their orbital inclinations: this parameter shows not only short-term oscillation but also considerable long-period variation.8
We thus see that as averages are taken over more sequences the difference between the individual average values drops very rapidly, and the "average of the averages" itself departs little from the long-term mean value. The relatively large orbit-by-orbit variations in the orbital period will therefore even out very quickly, before they are able to affect the super-period sequence, to give a mean value highly representative of the long-term average. I thus feel it is safe to say that the natural variations in the orbital period of Ceres will have little or no effect on the conclusions of the analyses described in the main body of this paper. Given that the other asteroids considered have sequences which are substantially more stable than those of Ceres, this same conclusion can be drawn in their case as well.
1 Mathematically speaking, this process of successive improvement can of course be taken as far as one wishes: each increase in accuracy takes longer and longer to arrive, however. The next "best answer" is 1123 conjunctions, made up of 6 times 153 minus 41, which has a periodicity of 8450yrs but a cumulative error of just 0.107 degrees. It makes only a very slight difference to the super-period, however, decreasing it to 1123/110 oppositions = 76.819yrs (a change of just 0.015%). Realistically though, even the hypothetical hyper-period is unlikely to have any true meaning, due to the influence of other sorts of perturbation, and so to go beyond this is totally unjustifiable.
2 It is also possible for Ceres to have two consecutive conjunctions fairly close to perihelion but, due to its longer synodic period, these will be "after, then before". This difference is crucial: the reversal of the order also reverses the shape of the constituent sections of the graph, meaning that no extra peak is produced.
3 Meeus J., Mathematical Astronomy Morsels V, Willman-Bell, 2009, pp.159-160
4 http://nssdc.gsfc.nasa.gov/planetary/factsheet/jupiterfact.html
5 http://hamilton.dm.unipi.it/~astdys/
6 Meeus J., Mathematical Astronomy Morsels, Willman-Bell, 1997, p.194 [N.B. This is the first volume in the series, also known as "Morsels I"]
7 Meeus J., Mathematical Astronomy Morsels V, Willman-Bell, 2009, p.156, para.2
8 ibid, p.163, para.6