
As mentioned on the page laying out the basic theory of eclipses, the position of the Moon's orbital nodes is not fixed in space: in fact the imaginary line connecting them rotates clockwise in the plane of the Earth's orbit by one revolution in 18.60yrs. As this is in the opposite direction to that in which the Earth orbits the Sun, the interval between the times when a given node is exactly between the Earth and the Sun is not a year but just 346.62 days i.e. one node or the other aligns every 173.31 days. One might think this would make eclipses very rare (as 177.18 clearly does not equal 173.31) but fortunately the Moon does not have to be precisely between the Earth and Sun for an eclipse to happen: the Earth is large enough so that even if the alignment is a little off, the Moon's shadow will still strike the Earth somewhere. In fact, if we include partial eclipses and consider the most favourable case (both Sun and Moon at their greatest apparent size), the maximum allowable error for a solar eclipse is about 1.58 degrees above or below the perfect alignment point. Because the tilt of the Moon's orbital plane is relatively slight (about 5deg 17mins at the time of an eclipse), this means that the node can be almost +/-17.4 degrees away from the Earth-Sun line (in the direction along the plane of the Earth's orbit) and there can still be an eclipse. The overall "window of opportunity" within which an eclipse could occur is thus 34.7 degrees. Repeating the above calculations for the least favourable case (both bodies at their smallest apparent size) gives a window of 30.9 degrees: this is the arc within which an eclipse of some sort must occur. Similar calculations can be done for total eclipses only, giving the values 22.5 (could) and 19.9 (must). These pairs of numbers are known as the major and minor ecliptic limits for partial and total solar eclipses respectively. The calculations involved in deriving accurate values for these limits, and also those for lunar eclipses, are surprisingly complicated so are laid out (in considerable detail!) in a separate article, which those with too much time on their hands should read when they return to the Astronomical Theory main index.
Each time a node returns into alignment with the Earth-Sun line, the Moon will need to travel on for another 3.87 days (177.18 minus 173.31) until it is new again i.e. before the next eclipse can occur. In this time the node will have moved almost exactly 4 degrees from its previous position. A series of eclipses will thus start near the beginning of the window of opportunity and steadily move closer to its end by 4 degrees each 177-day period. Because for an eclipse to be total the Moon must be near the centre of the window (as only there is the alignment sufficiently exact), the sequence will start with partials, then move on to totals/annulars and then finish with partials again - in fact just over one-third of eclipses are partial. Note also that because even the smallest window for partial eclipses (30.9deg) is larger than the angle the nodes move in the time between new Moons [if only just - the nodes actually move by 30.67 degrees!], every solar eclipse season must actually produce an eclipse of some type - if the Moon wasn't sufficiently near to a node at the 177-day mark it must have been so just one lunar month earlier.
Having travelled through the window in 4deg increments, the Moon will eventually get sufficiently close to its end that the alignments will allow an eclipse to occur after about 148 days (i.e. five new Moons, five and a half node crossings) instead of 177, allowing the eclipse series to flip from the end of the window back to the beginning. When this happens, if that eclipse is sufficiently close to the beginning of the window the next new Moon can still be within the window and so a further eclipse can happen just 29 days later. Most of these eclipses will be partial, however, as they occur near to either the start or the end of the window. The most extreme case is a year with five solar eclipses, where there are two pairs of 29-day events: this last happened in 1935 but will not do so again until 2206. Of the five, only either the first or last will be non-partial. It is easy to show that five is the most theoretically possible because a 29-day event will (almost!) always be both preceded by and followed by a 148-day event: a series of five eclipses must therefore have the interval sequence 148 29 148 29 (or the reverse) which adds up to 354 days and so no more are possible in that year. [In the rare occasions when the second 29-day event is not followed by a 148-day event, that next event will be a 177-day one and so the overall conclusion still holds.]
Note that the "flip" mentioned above will happen after five or six 177-day periods, not the eight or nine you might expect (34.7 divided by 4), because if an eclipse is near the end of the window then a 148-day event can happen and if it is near the start a 29-day event is possible. The effective window to be spanned by 177-day events is thus actually at most only 221/2 degrees, and can be as little as 181/2 if the sequence starts some distance inside the window (determined by the previous 148-day event). It thus takes just five or six lots of 4 degrees to move outside the window.
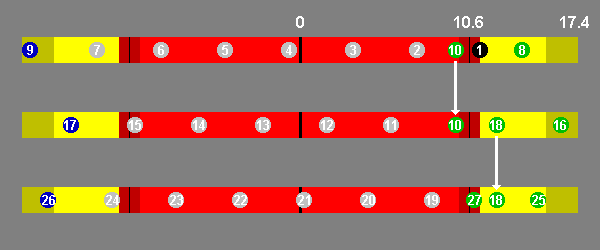
Perhaps a few diagrams would help here. Those below are to scale in the horizontal direction and each represents the "window of opportunity", centred on the point of perfect alignment (marked by the black line at zero) - the window extends almost 17.4 degrees in each direction i.e. 34.7 degrees in total, as given above. The yellow sections indicate that an eclipse with the Moon in this part of the window will be partial, the red shows that an eclipse here will be total (or annular). The smaller dark yellow and dark red areas mark variations in the limits of the window due to the effect of changes in the apparent size of Sun and Moon - remember that right at the start of this discussion I said that the 34.7 degree arc only applied if both Sun and Moon were at their largest. If both are at their smallest the arc is considerably reduced (by almost 2deg on each side, in fact - the width of the dark yellow areas). Thus if the Moon is in the dark yellow area, whether an eclipse will actually happen depends on the relative sizes of Sun and Moon at that time. If the Moon is fully within the bright yellow area an eclipse is certain, irrespective of size. A similar argument applies for the partial/total decision: within each dark red sector (width=11/3deg, centred on 10.6 degrees) the eclipse may be partial or total but in the bright red area it is guaranteed to be total (or annular, of course). Grey symbols indicate 177-day events, green ones 148-day events and blue ones 29-day events.

Let us start with the Moon at position 1 within the window: this will produce a certain partial eclipse (I am taking the right-hand edge of the circle as determining its position). After 177 days, the Moon has moved 4 degrees through the window relative to the node (as stated above) and so will now be at position 2: this will be a total eclipse. In successive 177-day periods the Moon will move to positions 3 to 6 (all total eclipses) and then finally to position 7 (partial). Crucially, the Moon is now far enough along the window to already be back within it after only 148 days: this is indicated by position 8, and gives a partial eclipse. Note that this return to the beginning of the window (the "flip" mentioned previously) would not have been possible until position 7 as before then the Moon would have been outside the window [to its right, in fact] after 148 days and so would have had to make a further orbit (29days) thus producing a 177 day interval.
Having reached position 8, there is (in this case) just enough room for the Moon to still be in the window after only another 29 days: this takes us to position 9. As this is in the dark yellow sector, whether an eclipse does actually happen will depend on the relative sizes of Sun and Moon. If all is well, we get a partial eclipse. If not, we must wait a little longer! In either case, another 148-day "flip" will now occur, taking us to position 10: probably a total eclipse but it might only be partial as it's inside the dark red sector. In terms of intervals, we have now had 177 x 6, then 148 29 148 or 148 177 depending on whether there was an eclipse at position 9 or not: both these patterns are seen in actual eclipse sequences.
For clarity, we now move on to the second diagram, indicated by the arrow between the two positions 10. Things proceed much as before, but because 10 is nearer to the centre-point than 1 we now only need five 177-day intervals to take us to position 15 (illustrating the point about the window for 177-day events made above). A "flip" will now occur (to position 16), but this lands in the dark yellow sector so we might not get an eclipse. If we do, the Moon will still be in the window 29 days later (position 17), yielding the sequence (177 x 5) 148 29. If there is no eclipse at position 16 then we just go directly from 15 to 17 with the sequence (177 x 5) 177. Whichever route we use to get to position 17, the next interval will be 148 days, giving the certain partial eclipse at position 18. In total, therefore, the sequences have been (177 x 5) 148 29 148 or (177 x 6) 148. Note that if there was no eclipse at position 16 what would have been a 148-day "flip" after five 177-day intervals has been converted into one after six: this effect reduces the number of "5's" below what one would expect simply from considerations of the window-width (but also see below!).
The third diagram illustrates two more issues. After moving from 18 to 24 by 177-day intervals, we then get back to position 25 with a 148-day event. As with the first diagram, position 18 was sufficiently far to the right that it took six 177-day intervals to be in a position to get a 148-day event. Now note that at position 25 the Moon is exactly on the border of the certain eclipse / possible eclipse line, but it is on the correct side of it so we do get an eclipse (a partial). There is then barely enough room for a 29-day interval, to take us to position 26, but the critical thing is that there is indeed enough room - just! This means that there must be an eclipse at either 25 or 26 (or both). If 25 were a little to the right (i.e. no eclipse) then 26 would be a certain eclipse and if 26 were a little to the left (no eclipse) then 25 would be certain. This guarantees that every eclipse season will produce a solar eclipse (as stated above), even if the relative sizes are at their most unfavourable (i.e. the inner-most edges of the dark yellow sectors come into play).

I drew the above diagrams from an arbitrary start point, and it just so happened they showed most of the points I wanted to illustrate. Because of the precise placement required, however, they did not show the "five in a year" sequence of 148 29 148 29 - I thus constructed a diagram to demonstrate this. This begins at 1 again (which would itself have been the result of a 177-day event) then proceeds to position 6 via the required sequence. Note that position 5 is (just!!) valid - don't forget I'm taking the right-most edge as the position. The only possible interval after 6 is 177 days, which takes us to the final position, 7. As the placements are so close, in "real-life" this sequence will usually only happen through a particular combination of events: either via the process I call "lead/lag" (see below), which effectively extends the width of the window somewhat, or due to the eccentricity of the Moon's orbit causing it to move slightly faster at the vital time (and thus stay within the window).
It is actually possible to have a run of seven 177-day periods but this requires special circumstances. If at the time a 148-day event would normally have happened the Earth is a little less far round its orbit than average it will have to move further before the nodes regain their orientation with the Earth-Sun line. The node re-alignment interval will thus increase slightly and so the time to the next new Moon (being the difference between the approx 173.3-day node re-alignment interval and the 177-day eclipse season) will decrease slightly, meaning that the nodes will shift by a smaller amount in this period. The Moon will thus need to move a correspondingly smaller distance through the window before it is new (and can cause an eclipse), possibly leaving insufficient room for the 148-day event to occur - an extra 177-day event will happen instead. Such a variation in orbital position can be caused by a variation in orbital speed due to the eccentricity of the Earth's orbit: the Earth goes a little quicker than average when nearer the Sun, and slightly slower when further away. From [currently] January to July the orbital position of the "true" Earth is thus ahead of that of the "mean" Earth, then from July back to January it lags behind - this can make almost +/-2deg difference. The maximum lag happens in early October, so if a 148-day event was due to occur around this time there is likely to be a "177 by 7" occasion instead. The last times this happened were 12th October 1996 and 11th September 2007, but the next won't be until 21st September 2025. This mechanism can also produce a run of five 177-day periods instead of six (or, exceedingly rarely, even four instead of five!), but for the converse reason - when the Earth is "running ahead" (in early April) the Moon must move a little further through the window and thus potentially bring forward a 148-day event. Because a run of five can also come about quite normally (see above) it's not easy to tell when one has been caused by "running ahead" - the next is probably on 13th March 2192. This also means that, overall, "177 by 5" will happen considerably more than "177 by 7". This is born out by data from actual eclipses: in the period 1900-2599 there were six times as many 5's as 7's (but a lot more 6's).
Lead/lag has one last oddity to show us: how can the sequence 148 177 29 148 happen? One might ask why, if the 29-day event is possible after the 177-day one, why was it not possible before it? The answer is that if the Earth is "leading" when the 29-day event was due there may not be enough of the window left for it to occur. However, after 177 days the Earth will now be "lagging": this switch from lead to lag can make 4deg difference in its actual position compared to the mean, which can be enough to allow for a 177-day event in between and still just fit in a 29-day event. This is made more possible by the observation that, because the time between successive new Moons is not constant (due to the variation of the Moon's speed in its non-circular orbit), "177-day" events do not all take exactly 177 days. A series of shorter-than-average new Moon periods can combine to produce an event significantly less than 177 days, which will not move the eclipse sequence so far through the window as a standard-duration event. Despite apparently needing several coincidences of circumstance for all the above to happen, between the dates given above it actually does so slightly more often than "177 by 7" occasions - the next time won't be until 2098 though.
Due to the complex way the orbits of the Moon and Earth interact, the magnitude of the lead/lag effect is not constant but changes over the centuries with a periodicity of, at the moment, about 565 years. When "177 by 7" events are more common "177+29" events are less so (and vice-versa). Such things as the number of eclipses, the distribution of years with five solar eclipses and instances of four successive total lunar eclipses are also affected by this periodicity, as they all depend on the lead/lag effect.
If you're not convinced by this "window and flip" business, then things can be viewed from a timing perspective. Although the time difference between the six new Moons and six-and-a-half node-crossings associated with a 177-day period is not great (+0.304days), it would eventually accumulate to the point where things got too far out of step for an eclipse to happen were it not compensated for by the difference of -2.014days you get with 148-day events (negative because five new Moon periods are less than five-and-a-half node crossing periods). Were it not for 29-day events, one 148-day event would compensate for six or seven 177-day events but as 29-day events have a large time difference (+2.318days) the formula to achieve a close compensation is actually 1x29 plus 2x148 plus 6x177 [ 1 x (+2.318) + 2 x (-2.014) + 6 x (+0.304) = 0.114days ]. This ratio (1:2:6) is precisely that of the most common arrangement of intervals between eclipses derived above using the "window of opportunity" method (177 x 6 148 29 148): this shows that the two approaches are equivalent. However, because you can sometimes get patterns such as 148 29 148 29, and a run of five 177's instead of six, there are actually slightly more 148's and slightly less 177's than given by the simple "whole-number" ratio: the exact values are in fact 1.000:2.047:5.933. Using these figures, the sum comes to just -0.000131days i.e very close to perfect compensation.
The compensation effect ensures that, averaged over a large number of cycles, new Moons will indeed coincide with a node crossing (or very nearly so), this being the requirement for an eclipse to happen. That this is actually what's going on can be tested by data from real eclipses. If you take the 1347 eclipses in the 568yr period between 2032 and 2599 and put the number of 29-day, 148-day and 177-day intervals into the compensation sum given above, the overall result comes out to just less than -0.02days i.e. after that large number of eclipses spread over approaching six centuries, things are out of step by only 28minutes! And why did I choose that interval of years? Because of the long-period variability mentioned in the section immediately above this one: selecting an arbitrary number of years could distort the percentages of the three eclipse intervals and thus affect the result. The period is not exactly 565yrs because I also had to ensure the count started and ended at the same point in the basic 177x6 148 29 148 cycle as this too would affect the percentages.
Note that compensation does not happen smoothly, but rather in jumps - for example, the six 177-day intervals will put things more and more out of sync before the timing is dragged back the other way by a 148-day event. The cumulative timing error at a given eclipse will thus fluctuate considerably, but only within certain bounds. By finding these bounds one can determine the "timing compensation" version of the ecliptic limits. Using the time differences given above, I calculated the predicted cumulative timing error for each eclipse in the sequence of all 1643 eclipses between 1901 and 2599 and determined the overall maximum and minimum values. I found that the maximum error (positive or negative) at a given eclipse averaged out at 1.515days i.e. the new Moon could be up to 1.515days away from a node at the time of the eclipse. The difference in longitude this represents is 18.39deg - consideration of whether this value is in accord with theory must wait until a later section though!
We have seen that the time between two successive eclipses is approximately 177, 148 or 29 days, caused by alignments after 61/2, 51/2 and 1 node-crossing intervals respectively. However, the plane of the Moon's orbit of course intersects the plane of the Earth's orbit at two places so there are two nodes. At one of these nodes the Moon will be moving in a downwards direction and at the other it will be moving upwards - the two intersections are thus called the "descending" and "ascending" nodes respectively. Now the node-crossing interval referred to above is specified relative to one particular node (either descending or ascending) so the physical meaning of an alignment happening after "half an interval" is that the alignment will be with the other node. It should thus be clear that eclipses separated by 177 or 148 days will happen at different nodes while those separated by 29 days will happen at the same node.
Right at the start of this page I said that the Moon could be either above or below the perfect alignment point and an eclipse still happen. If we take the view that "up" means "to the north" then I hope it will be clear that the point where the Moon's shadow strikes the Earth when the Moon is above the perfect alignment point will be in the northern hemisphere and when it is below it will be in the southern hemisphere. Note that I didn't say north or south of the equator, because the position relative to the equator will depend on the tilt of the Earth's axis at the time of the eclipse. One can say north or south of the centre of the Earth, however, as this clearly doesn't move. Which leads us to the next "technical term" - gamma value. The gamma value of an eclipse is a measure of how far the centre-line of the eclipse passes north or south of the centre of the Earth, in units of the radius of the Earth. By convention, eclipses passing to the north have positive gamma values and those passing to the south have negative gamma values. A perfectly-aligned eclipse has a gamma value of zero as its centre-line passes directly through the centre of the Earth. One would think that the gamma value for the case of a total eclipse just grazing the Earth would be (+/-) 1.00 i.e. one Earth-radius from the centre, but due to the fact that the Earth is not a perfect sphere it is actually about 0.9972. Eclipses with gamma values greater than 1 are possible of course - this just means that the centre-line misses the Earth entirely and so nowhere is the eclipse total i.e. they are "true" partial eclipses (as opposed to being partial because the observer is too far away from the centre-line track). The largest gamma value for which an eclipse may just happen is about 1.57 i.e. the centre of the shadow-cone can miss the Earth by over 2200mls! This shows how large the penumbra is compared to the umbra and justifies the statement that the alignment does not have to be exact.
Now we have done some groundwork it's time for another diagram, showing the four possible combinations of node type (descending or ascending) and position (eclipse before Earth reaches the node or after it has passed it) as viewed along the Sun-Earth line. The dark circle represents the Earth, the light one the Moon and the lines are the orbital paths: the node is the point where these cross. Although not shown with an arrow, the Earth will be moving from right to left, the opposite way from the Moon. It will thus be yet to reach the node if it is to the right of the node and past it if it is to the left of the node.
Eclipse is before Earth reaches node | Eclipse is after Earth has passed node | |
|---|---|---|
| Moon at descending node | 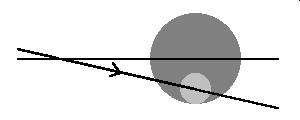 | 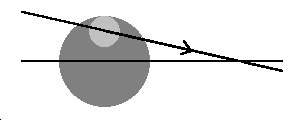 |
| Moon at ascending node | 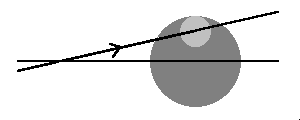 | 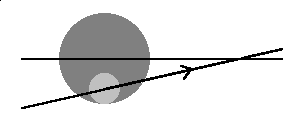 |
We can see that for a given position relative to the node, whether the eclipse will have a positive (northerly) or negative (southerly) gamma value depends on whether the Moon is at a descending or ascending node. Relating this to the first conclusion drawn above, that successive eclipses separated by 177 and 148 days will be at different nodes, it follows that a series of 177-day eclipses will have gamma values that alternate between positive and negative even though their position in the window is moving smoothly from one side to the other ("lead/lag" not withstanding!). This has consequences for the next part of the discussion!
More confirmation of the equivalence of the "window" and "timing" approaches came when I plotted the calculated timing error and gamma value for each eclipse in the period 1900-1999 on the same graph. Before doing this, however, I had to deal with the issue mentioned above - the gamma values for successive 177-day eclipses jump from positive to negative and back for reasons that have nothing to do with the phenomenon we are trying to demonstrate. To avoid this problem, I noted that the symmetry of the situation dictates that eclipses occuring at the same position relative to the node but with different node types will have equal gamma magnitudes but opposite signs. Mathematically, it is therefore perfectly valid to reverse the sign of alternate 177-day eclipses before doing the plot - effectively reducing them all to descending (or ascending) node events. A similar process can be carried out for 148-day events: these can never be in sequence but will often be before or after 177-day events and thus subject to the same positive/negative alternation.
The above adjustment sorts out the "jumping around" problem but to make a sensible plot we've still got to make sure that positive and negative window-position values correspond to positive and negative gamma values. It seemed logical to give window positions after the perfect-alignment point positive values, and from the above diagram it can be seen that it is descending node eclipses that have positive gamma values when the eclipse is after the the perfect-alignment point (i.e. the node). I thus chose to reduce all eclipse gammas to the equivalent descending node values before plotting against the timing error.
When I used the "corrected" gammas, scaled to the same range of values the two plots were almost identical. This is highly significant because, as I said above, the gamma value indicates how "central" the eclipse is. A value of zero means the centre-line of the eclipse goes straight through the centre of the Earth, which can only happen when the Moon is exactly at a node i.e. is in the centre of the "window of opportunity": we now see this corresponds to a timing error of zero. Conversely, a large gamma value means the eclipse has only just grazed the edge of the Earth i.e. is right on the edge of the window, with a correspondingly large timing error.
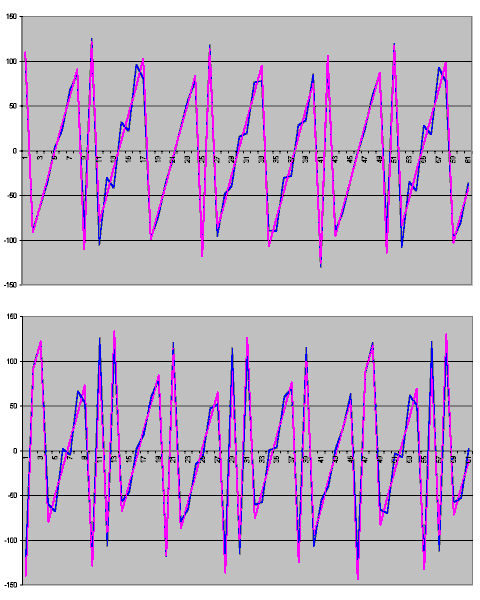 | For the two plots to be identical, the "cumulative timing error" method must be an accurate predictor of where an eclipse will be located within the window. To check my results I repeated the process for eclipses in 2000-2099 and 2300-2399: portions of the plots for each century are shown on the left - timing error is pink, gamma is blue. The outcome was the same - identical plots - but each of the pairs of graphs was subtly different. The most obvious difference was that the 2300-2399 plot (lower graph) had more large values - in eclipse terms this means more "marginal" eclipses (those that just squeeze into the window of opportunity). This is actually an expected result because the period 2300-2399 is in the part of the 565yr cycle that has many more 29-day events. Eclipses separated by 29 days must fall towards the edges of the window (as the window is, on average, only 33.3 days wide) so will have high gamma values. Note also that a greater number of 29-day events will tend to produce more eclipses overall but they will mostly be partial due to being at the edges of the window. This is borne out by the data: while there are 23 more eclipses in 2300-99 compared to 1900-99 only 6 of these are totals. |
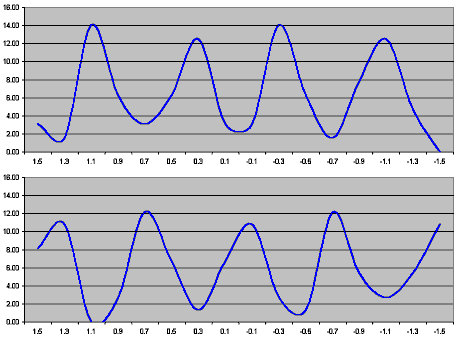 | Further "playing around with the numbers" produced a totally unexpected result, however - for each of the centuries from 1900 to 2500 there are values of gamma which are heavily favoured over others, by a factor of around 7 times: see the (smoothed) plots of gamma-value distribution for 2000-2099 and 2300-2399, left. The favoured values are different in each century but the overall shape of the distributions is the same - a fairly regular "wave" with four maxima. The period from peak to trough averages out at about 0.36 so the peak to peak interval is 0.72. This can be converted into a corresponding distance within the window by firstly observing that, numerically, the maximum gamma value is almost exactly the same as the solar ecliptic limit in latitude: 1.547 compared to 1.579 i.e. a difference of 1 "gamma unit" corresponds to a difference of 1.02deg in latitude. Thus 0.72 gamma units is 0.734deg. Using the model I derived for calculating ecliptic limits this converts to a difference of exactly 8deg of longitude, or twice the distance an eclipse will move through the window of opportunity after a "standard" 177-day interval. |
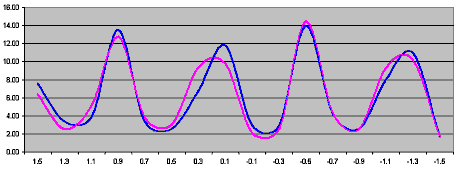 | That the variation between centuries is a result of the 565yr cycle was clearly shown by the way that gamma-value distributions for centuries at equivalent points in the "upswing" and "downswing" of the cycle were found to be very similar: the graphs for centuries starting in 2200 & 2300, 2100 & 2400 and 2000 & 2500 were almost perfect duplicates That on the left shows 2100-2199 (pink) and 2400-2499 (blue). |
The mechanism for the occurence of favoured values is our old friend "lead/lag". Due to this effect, a pair of eclipses occuring in April and October will be much closer together in the window than average because the April event will be further through the window than the mean figure would indicate while the October event will be less far through. Conversely, October/April pairs will tend to move apart while such pairs as January/July will stay at the nominal spacing (as lead/lag is virtually inoperative then). This will cause a bunching effect, which will be reflected in the gamma values. Note that bunching happens as a result of the members of pairs of eclipses moving towards or away from each other. Given that each eclipse is separated by 4deg initially the centre-to-centre distance between two pairs is clearly 8deg, and this will remain so if the members of each pair move symmetrically to produce the bunches (as they are assumed to do in this case). This explains the distance between the bunches described above. Which values are favoured will depend on where the individual eclipses sit within the window, and this is determined by the sequence of intervals as different sequences have different numbers of eclipses within them and span different distances in the window. This latter factor is particularly important because if a sequence has a large span it can only fit in the window if centred on a small range of values whereas a sequence with a smaller span has much more freedom to place itself at various points within the window.
But if only it were that easy! I'm sure you wouldn't expect there to be an entirely straightforward answer to any question concerning eclipses, and the orbit of the Moon in particular, so I'm afraid it's time for another (rather lengthy!) diversion into the depths of the arcane. As ever, those in a hurry should just keep reading but if you want to be considered an expert you've just got to click here.
Rather a long way up this page now, I said that the line of nodes was not fixed in space but moved round the Moon's orbit in the opposite direction to the Moon itself, completing one revolution in 18.60yrs. This may have seemed like a bad thing, but read on ....
If the line of nodes was fixed in space then the node re-alignment interval would be 182.62 days (i.e. exactly 6 months) and of course this number is even further from 177.18 than 173.31 is! In this case successive eclipses would move 5.65deg through the window of opportunity, but in the opposite direction from now, resulting in radically different patterns of eclipses. For an exact match between node re-alignment period and eclipse season the line of nodes would have to revolve once in 32.58yrs. As this interval determines the node-crossing period (known as the draconic month) this would change as well, becoming 27.26 days. Now here's the interesting bit! Remember we said earlier that eclipse seasons come about because six full Moon periods were very nearly equal to six and a half node-crossing periods? Well, with the new value for the draconic month the two numbers are not just close they are exactly equal! If everything fell exactly right, the result of all this would be a total/annular eclipse every eclipse season (rather than the mix of partials and totals we get now) as there would be no movement through the window of opportunity. However, as every eclipse would be exactly at the centre of the window there would be no 148 or 29-day events: these are only possible at the borders of the window. This means there would be fewer eclipses in total - a decrease from the 2.38 per year now to 2.06, in fact. In addition, eclipses would be visible in a somewhat narrower region than currently: eclipses visible at high latitudes are generally those sitting away from the centre of the window. However, as all of the 2.06 eclipses per year would be non-partial (compared to just 1.54 per year now) the above might constitute an acceptable trade-off! Problem is, this scenario is incredibly unlikely because with all the various periods locked together it is overwhelmingly more probable that the Moon would be permanently nowhere near a node at new Moon rather than always at a node. Maybe not such a good idea to slow the line of nodes down after all!! Just goes to show that a certain degree of imprecision in these things is not a bad idea - perfection may then not happen all the time but at least it will do so sometimes.
If you thought that was the end of the huge list of complications, think again! In the main, the above discussion dealt throughout with nice neat numbers: full Moons happen every 29.53 days, the nodes re-align every 173.31 days etc. etc. This is often a reasonable way to deal with things because, on average, these numbers are indeed accurate. However, as briefly mentioned in the section on "lead/lag", average values don't tell the full story: we must sometimes deal with the values pertaining to a particular orbit, not those averaged over many orbits.
There are several reasons why "actual" values might differ from average ones. The easiest to understand is the one mentioned previously: a body in an non-circular orbit does not travel at the same speed at all points in its orbit - it moves more quickly when nearer to the parent body. Less obvious is the fact that when you have more than two bodies involved, the interactions between them distort the paths that simple geometry tells you they would follow. This is particularly true for the Moon, which has one of the most complex orbits in the entire solar system! Due to the sometimes opposing and othertimes additive influences of the Sun and the Earth (and other planets, to a minor degree), no parameter of its orbit is constant. Importantly for the discussion of eclipses, the position of the nodes moves around continually (but only by a small amount, fortunately!).
The node defined by the parameters of a particular orbit is called the True Node, and that derived from average values is called the Mean Node. It is the true node which is important for an eclipse, because of course an eclipse happens on a given orbit not at some average time. However, all calculations are implicitly done using the mean node because mean values are used for the various times, angles etc. It is often more helpful to quote such things as ecliptic limits relative to the mean node as the mean is easier to determine. We thus need to know exactly how the true node behaves.
The orbit of the Moon has been studied for millenia but it is only surprisingly recently (in the last 20yrs or so) that sufficiently detailed mathematical expressions have been available that allow us to accurately determine its position. If the expression for the nodes is plotted from day to day on a graph, the true node is seen to follow a wavy line centred on the straight line representing the mean node. The major "waves" are nicely regular though, with a period of 173.3 days (recognise that figure from somewhere?). A little thought should convince you that should a perfectly-aligned eclipse occur, the true node (which specifies where the eclipse actually happens) and the mean node (which specifies where the eclipse should ideally happen) must be at the same place i.e. the eclipse will occur at one of the points where the wavy line crosses the straight line. Extending this argument just a little, we may therefore say that all eclipses will occur near to crossings. This enables us to relate the data from the graph to the circumstances of actual eclipses and thus deduce which crossings are the relevant ones.
When I did this (taking my data for the true and mean nodes from a program designed for astrologers, would you believe?!) I was able to prove that around the time of an eclipse the mean node was always further away from the Moon than the true node, whether the eclipse was before or after the "perfect" point. This means that windows of opportunity measured relative to the mean node will always be larger than those measured relative to the true node (i.e. those given at the top of this page). The actual difference depends on the shape of the "wavy line" and the distance from the perfect point, so I calculated two values: one for the solar major limit (17deg 24min) and another for the lunar major limit (11deg 29min) - the values here are those quoted by Meeus. This gave "mean node" limits of 18deg 17min and 12deg 5min respectively, compared to Meeus' values of 18deg 24min and 12deg 8min. The small discrepancy is almost certainly because the exact shape of the "wavy line" changes on timescales of years as well as days so the true/mean difference will change a little depending on the year used to plot the graph. To check this, I scaled the difference between the true and mean values so that its maximum became equal to the maximum amplitude of the "waves" as given by theory: the derived answers were then correct to within 1min of arc. QED, I think. We can now give an answer to the question about "timing compensation" ecliptic limits posed somewhat earlier. The value I derived was 18.39deg. This was calculated by the use of average time differences for each of the eclipse intervals so it is actually a "mean node" result. If I adjust my value for the "window of opportunity" version of the solar major ecliptic limit (17deg 24min) to convert it to a mean node value, the answer is 18.38deg (18deg 23min). The extremely close agreement of the values again shows that the "window of opportunity" and "timing compensation" methods are indeed equivalent ways of looking at the same situation.
And if you're wondering whether this true/mean business affects other eclipse parameters - yes indeed it does! For example, although the average tilt of the Moon's orbit is 5.145 degrees it can vary from 5.304 to 4.981. As with the nodes stuff, I did some detailed research into the matter (using an unbelievably complex formula for the Moon's position) and was able to show that at eclipses the tilt would always be at (or very near to) its maximum value. Similarly, the closest and furthest distances of the Moon from the Earth [perigee and apogee] vary quite a bit from orbit to orbit (by over 3.5% in the case of the perigee) but the effect this has on eclipses is largely masked by the much greater variation caused by where the shadow strikes the Earth's surface (and of course the nearer the Moon gets the faster it moves, thus undoing much of the advantage of its apparent size being larger).
Due to the different geometry involved, even under the most favourable circumstances the "window of opportunity" for partial and total umbral lunar eclipses is only 23 degrees wide. As this is less than the angle moved by the nodes in a lunar month, not every lunar eclipse opportunity will actually produce an [umbral] eclipse: lunar eclipses are thus less common than solar eclipses, by a factor of almost 0.65 (best calculated by considering the average window because, as stated above, the possibility that an eclipse will occur depends on the relative sizes of Sun and Moon as seen from the Earth, not just the basic geometry). The upside is that an eclipse of the Moon is visible from the entire night-time side of the Earth. In addition, because the window of opportunity is narrower than the movement of the nodes in both 29 and 148 days, it is not possible to have two [umbral] lunar eclipses separated by either of these periods, as it is for solar eclipses. It therefore follows that the maximum number of [umbral] lunar eclipses in a calendar year is three, each separated by 177 days. The longest period without an umbral lunar eclipse is 679 days, made up of periods of 177, 148, 29, 148 & 177 days: during this period, all [four] eclipses are penumbral. The last time this happened was from 5th July 2001 to 16th May 2003, the next will be 28th Sept. 2015 to 17th August 2017.
The greatest possible number of consecutive total lunar eclipses is four - this is known as a Lunar Tetrad. Tetrads are only possible because of the lead/lag effect discussed in connection with unusual solar eclipse sequences, and their frequency of occurence over time is very variable as they are one of the phenomena affected by the 565yr periodicity mentioned earlier. We are currently about in the middle of a time period where they are relatively plentiful, however - 17 "sets" occur from 1909 to 2156. The most recent Tetrad began on 15th April 2014 and will end on 28th September 2015. The next one after that will begin on 25th April 2032 (spot the Saros Period interval between them!). It was a study of Tetrads that brought to light the long-term variability of many eclipse phenomena. The period of this variability is currently 565yrs but in fact it is slowly decreasing with time according to the formula P = 565.1 - 1.38*T, where T is the number of centuries from the year 2000. It is not entirely clear why this periodicity should exist, but the best theory relates it to a slight variation in the Earth's orbital position caused by one of the many subtle interactions between Sun, Earth and Moon.
The original study used historic lunar eclipse data centred around the year 479AD. At this time the periodicity would have been 586yrs, an interval which became known as the Tetradia because of this study. The Tetradia is also an "eclipse cycle" i.e. an interval after which many aspects of eclipses will repeat almost exactly, and has a further significance in connection with the numbers of eclipses in what are known as "Saros Series". I have examined Saros Series in great detail, and have recorded my work in another article in this section. You will be able to link to this page just after you get back to the main page, so I shall not attempt any further explanations at this point.
From the information above, one might imagine that the maximum total number of eclipses of either type in a [calendar] year would be eight (five solar and three lunar). However, solar and lunar eclipse opportunities happen alternately and it is not possible for there to be a lunar eclipse between two solar eclipses separated by 148 days, as during this period the Moon is far from a node. So, taking the sequence of intervals associated with five solar eclipses (148 29 148 29) it is only possible for a lunar eclipse to happen during the 29 day intervals, to give this sequence of seven eclipses in 356 days:- S/148/S/15/L/15/S/148/S/15/L/15/S. The other way a total of seven can occur is with four solar and three lunar, based on the 177 148 29 148 177 sequence of solar eclipses seen in 2000. This gives L/15/S/148/S/15/L/15/S/148/S/15/L. The next case of "5 plus 2" will be in 2206, the next "4 plus 3" being in 2094. Note however that in the periods 21st Dec 2010 to 10th Dec 2011 and 31st Jan 2018 to 21st Jan 2019 there will be 4 solar eclipses (all partial) and 3 lunar (all total): examples of the rather more common case of "4 plus 3" in the space of 12months rather than a calendar year.
Because the lunar eclipses in the middle of these sequences must occur very near the centre of the eclipse window (as they happen between 29-day solar eclipses, which are always close to the ends of the window), they will always be total - in fact the Moon will often pass particularly close to the centre of the Earth's shadow, as in the case of 16th July 1935, 16th July 2000, 15th June 2011 and 27th July 2018.
All crystal clear, I trust?? Questions will be asked in due course.